1. 定义一种新运算“$\odot$”:$1\odot 3 = 1×4 + 3 = 7$,$3\odot 1 = 3×4 + 1 = 13$,$5\odot 4 = 5×4 + 4 = 24$,…$$. 观察各式,并解决下列问题:
(1) 计算$4\odot 3$和$a\odot b$;
(2) 若$a≠b$,那么$a\odot b$______$b\odot a$;(填“$=$”或“$≠$”)
(3) 计算:$-5\odot (-4\odot 3)$.
(1) 计算$4\odot 3$和$a\odot b$;
4⊙3=4×4+3=19,a⊙b=4a+b
(2) 若$a≠b$,那么$a\odot b$______$b\odot a$;(填“$=$”或“$≠$”)
≠
(3) 计算:$-5\odot (-4\odot 3)$.
-5⊙(-4⊙3)=-5⊙(-4×4+3)=-5⊙(-13)=-5×4+(-13)=-33
答案:
1.
(1)解:4⊙3=4×4+3=19,a⊙b=4a+b.
(2)≠
(3)解:-5⊙(-4⊙3)=-5⊙(-4×4+3)=-5⊙(-13)=-5×4+(-13)=-33.
(1)解:4⊙3=4×4+3=19,a⊙b=4a+b.
(2)≠
(3)解:-5⊙(-4⊙3)=-5⊙(-4×4+3)=-5⊙(-13)=-5×4+(-13)=-33.
2. 规定:求若干个相同的有理数(均不等于 0)的除法运算叫作除方,如$2÷2÷2$,$(-3)÷(-3)÷(-3)÷(-3)$等. 类比有理数的乘方,我们把$2÷2÷2记作2^{③}$,读作“2 的圈 3 次方”,$(-3)÷(-3)÷(-3)÷(-3)记作(-3)^{④}$,读作“$-3$的圈 4 次方”. 一般地,把$\underbrace{n个a}_{a÷a÷a÷...÷a}(a≠0)$记作 ,读作“$a的圈n$次方”.
,读作“$a的圈n$次方”.
(1) 直接写出计算结果: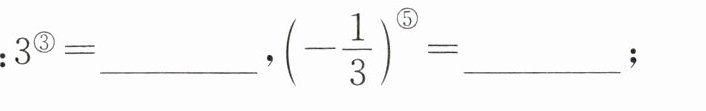
(2) 关于除方,下列说法错误的是______.
A. 任何非零数的圈 2 次方都等于 1

D. 负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
(3) 我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

① 试一试:仿照如图所示的算式,将下列运算结果直接写成幂的形式.

② 想一想:将一个非零有理数$a的圈n$次方写成幂的形式:______;
③ 算一算: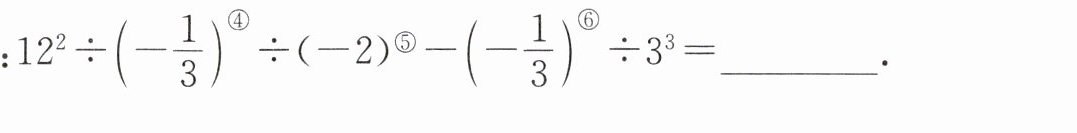
 ,读作“$a的圈n$次方”.
,读作“$a的圈n$次方”.(1) 直接写出计算结果:
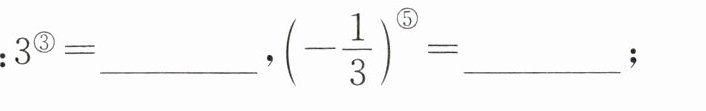
$\frac{1}{3}$
-27
(2) 关于除方,下列说法错误的是______.
C
A. 任何非零数的圈 2 次方都等于 1

D. 负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
(3) 我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

① 试一试:仿照如图所示的算式,将下列运算结果直接写成幂的形式.

$(-\frac{1}{3})^2$
$(\frac{1}{5})^4$
$(-2)^8$
② 想一想:将一个非零有理数$a的圈n$次方写成幂的形式:______;
$(\frac{1}{a})^{n-2}$
③ 算一算:
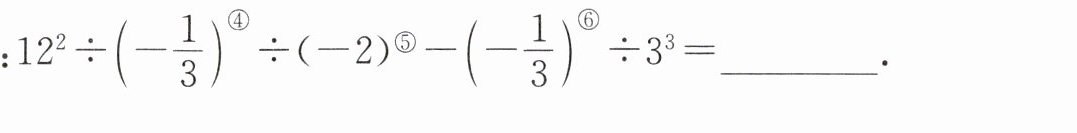
-131
答案:
2.
(1)$\frac{1}{3}$ -27
(2)C
(3)①$(-\frac{1}{3})^2$ $(\frac{1}{5})^4$ $(-2)^8$ ②$(\frac{1}{a})^{n-2}$
③-131
(1)$\frac{1}{3}$ -27
(2)C
(3)①$(-\frac{1}{3})^2$ $(\frac{1}{5})^4$ $(-2)^8$ ②$(\frac{1}{a})^{n-2}$
③-131
查看更多完整答案,请扫码查看


