《2025年启东中学作业本七年级数学上册苏科版徐州专版》

1. 如图,大长方形 $ABCD$ 是由一张周长为 $C_{1}$ 的小正方形纸片①和四张周长分别为 $C_{2}$,$C_{3}$,$C_{4}$,$C_{5}$ 的小长方形纸片②,③,④,⑤拼成,若大长方形的周长为定值,则下列各式中为定值的是( )

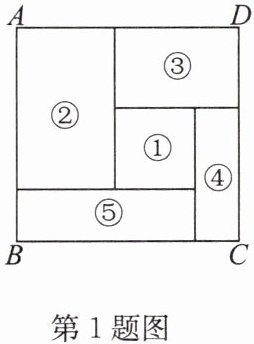
A.$C_{1}$
B.$C_{3}+C_{5}$
C.$C_{1}+C_{3}+C_{5}$
D.$C_{1}+C_{2}+C_{4}$

答案：
B　点拨:如答图,根据题意可知EF=FG=GH=HE,HN=MC,所以C₃+C₅=(OD+PF)+(BM+HN)+(OE+EF+BP)+(DN+GH+GM)=AD+BC+AB+CD.故当大长方形的周长为定值时，C₃+C₅为定值
　　　　　　　

2. 已知代数式 $A = 2x^{2}+3xy + 2y$,$B = x^{2}-xy + x$。
(1) 求 $A - 2B$；
(2) 当 $x = -1$,$y = 3$ 时,求 $A - 2B$ 的值；
(3) 若 $A - 2B$ 的值与 $x$ 的取值无关,求 $y$ 的值。

答案： 解:
(1)因为A=2x²+3xy+2y,B=x²−xy+x,
　所以A−2B=(2x²+3xy+2y)−2(x²−xy+x)=2x²+3xy+2y−2x²+2xy−2x=5xy−2x+2y.
(2)当x=−1,y=3时,
A−2B=5xy−2x+2y=5×(−1)×3−2×(−1)+2×3=−15+2+6=−7.
(3)因为A−2B的值与x的取值无关，
　所以5xy−2x=0,所以5y=2,解得y=$\frac{2}{5}$.

3. 将 5 张相同的小长方形纸片(如图①所示)按图②所示的方式不重叠地放在长方形 $ABCD$ 内,未被覆盖的部分恰好被分割为两个长方形,面积分别为 $S_{1}$ 和 $S_{2}$,已知小长方形纸片的长为 $a$,宽为 $b$。
(1) 当 $a = 7$,$b = 2$,$AD = 15$ 时,长方形 $ABCD$ 的面积是______195,$S_{1}-S_{2}$ 的值为______-29；
(2) 当 $AD = 20$ 时,请用含 $a$,$b$ 的式子表示 $S_{1}-S_{2}$ 的值；
解:因为S₁=(20−a)×3b,S₂=(20−2b)×a,所以S₁−S₂=(20−a)×3b−(20−2b)×a=60b−ab−20a.
(3) 若 $AB$ 的长度为定值,$AD$ 的长度不确定,将这 5 张小长方形纸片还按照同样的方式放在新的长方形 $ABCD$ 内。当 $AD$ 的长度改变时($AD ＞ a$),$S_{1}-S_{2}$ 的值总保持不变,则 $a$,$b$ 满足什么关系？
解:因为S₁−S₂=3b(AD−a)−a(AD−2b),整理,得S₁−S₂=(3b−a)AD−ab.因为AB的长度不变，AD的长度改变，而S₁−S₂的值总保持不变，所以3b−a=0,即a=3b.

答案： 3.
(1)195　−29
(2)解:因为S₁=(20−a)×3b,S₂=(20−2b)×a,
　所以S₁−S₂=(20−a)×3b−(20−2b)×a=60b−ab−20a.
(3)解:因为S₁−S₂=3b(AD−a)−a(AD−2b),
　整理,得S₁−S₂=(3b−a)AD−ab.
　因为AB的长度不变，AD的长度改变，而S₁−S₂的值总保持不变，所以3b−a=0,即a=3b.