1. 如图是一副特制的三角尺,仅用这副特制的三角尺不能画出的角度是(
A.$84^{\circ}$
B.$68^{\circ}$
C.$48^{\circ}$
D.$24^{\circ}$
B
)A.$84^{\circ}$
B.$68^{\circ}$
C.$48^{\circ}$
D.$24^{\circ}$
答案:
B
2. 如图,若将三个含$45^{\circ}$角的直角三角尺的直角顶点重合放置,则$∠1$的度数为

30°
。
答案:
30°
3. 已知将一副三角尺(直角三角尺$OAB和直角三角尺OCD$)的两个顶点重合于点$O$,$∠AOB = 90^{\circ}$,$∠COD = 30^{\circ}$。
(1)如图①,当$OC恰好平分∠AOB$时,求$∠BOD$的度数;
(2)如图②,在$∠AOC内部作射线OM$,使$∠AOM= \frac{1}{2}∠COM$,在$∠BOD内部作射线ON$,使$∠BON= \frac{1}{2}∠DON$,如果三角尺$COD在∠AOB内绕点O$任意转动,$∠MON$的度数是否发生变化?如果不变,求其值;如果变化,说明理由。
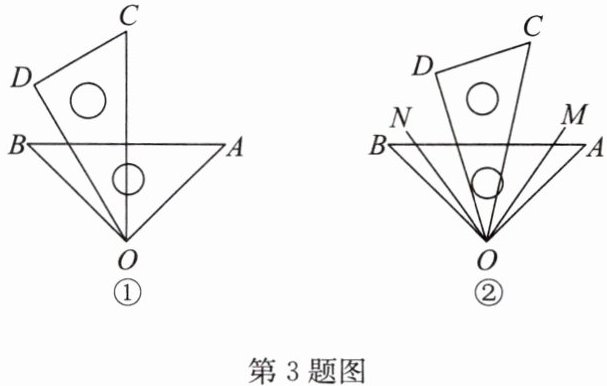
(1)如图①,当$OC恰好平分∠AOB$时,求$∠BOD$的度数;
(2)如图②,在$∠AOC内部作射线OM$,使$∠AOM= \frac{1}{2}∠COM$,在$∠BOD内部作射线ON$,使$∠BON= \frac{1}{2}∠DON$,如果三角尺$COD在∠AOB内绕点O$任意转动,$∠MON$的度数是否发生变化?如果不变,求其值;如果变化,说明理由。

答案:
解:
(1)因为 OC 是∠AOB 的平分线,∠AOB=90°,
所以∠BOC=$\frac{1}{2}$∠AOB=45°,
所以∠BOD=∠BOC-∠COD=45°-30°=15°.
(2)不变.因为∠AOB=90°,∠COD=30°,
所以 ∠BOD + ∠AOC = ∠AOB - ∠COD = 90°-30°=60°.
因为∠AOM=$\frac{1}{2}$∠COM,∠BON=$\frac{1}{2}$∠DON,
所以∠AOM=$\frac{1}{3}$∠AOC,∠BON=$\frac{1}{3}$∠BOD,
所以∠AOM+∠BON=$\frac{1}{3}$(∠AOC+∠BOD)=$\frac{1}{3}$×60°=20°,
所以∠MON=∠AOB-(∠AOM+∠BON)=90°-20°=70°.
(1)因为 OC 是∠AOB 的平分线,∠AOB=90°,
所以∠BOC=$\frac{1}{2}$∠AOB=45°,
所以∠BOD=∠BOC-∠COD=45°-30°=15°.
(2)不变.因为∠AOB=90°,∠COD=30°,
所以 ∠BOD + ∠AOC = ∠AOB - ∠COD = 90°-30°=60°.
因为∠AOM=$\frac{1}{2}$∠COM,∠BON=$\frac{1}{2}$∠DON,
所以∠AOM=$\frac{1}{3}$∠AOC,∠BON=$\frac{1}{3}$∠BOD,
所以∠AOM+∠BON=$\frac{1}{3}$(∠AOC+∠BOD)=$\frac{1}{3}$×60°=20°,
所以∠MON=∠AOB-(∠AOM+∠BON)=90°-20°=70°.
查看更多完整答案,请扫码查看


