《2025年启东中学作业本七年级数学上册苏科版徐州专版》

1. 由若干个小正方体堆成的大正方体,其表面被涂成红色,在所有小正方体中,三面被涂成红色的有a个,两面被涂成红色的有b个,一面被涂成红色的有c个,那么在a,b,c三个数中(D)
A.a最大
B.b最大
C.c最大
D.哪一个最大与堆成大正方体的小正方体个数有关

答案： D

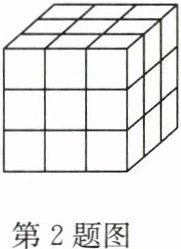
2. 如图,将一个正方体木块涂成红色,然后把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体,其中三面涂色的小正方体有8个,两面涂色的小正方体有12个,一面涂色的小正方体有6个,各面都没有涂色的小正方体有1个。现将这个正方体的棱n等分,如果得到各面都没有涂色的小正方体216个,那么n的值为______8。

答案： 8 点拨:由$(n-2)^{3}=216$,解得$n=8.$

3. 如图,下列几何体是由若干个棱长为1的小正方体按一定规律摆成的,若将露出的表面都涂上颜色(底面不涂色),观察这些几何体,探究其中的规律。
(1)第1个几何体中只有2个面涂色的小正方体共有4个；第3个几何体中只有2个面涂色的小正方体共有20个；
(2)求出第100个几何体中只有2个面涂色的小正方体的个数；
解:观察图形可知,题图①中,只有2个面涂色的小正方体共有4个;题图②中,只有2个面涂色的小正方体共有12个;题图③中,只有2个面涂色的小正方体共有20个.4,12,20 都是4的倍数,可分别写成$4×1,4×3,4×5$的形式,因此第n个图中只有2个面涂色的小正方体的个数是$4(2n-1)=8n-4$,则第100个几何体中只有2个面涂色的小正方体的个数是$8×100-4=796.$
(3)求出前100个几何体中只有2个面涂色的小正方体的个数的和。
解:根据题意,得$(8×1-4)+(8×2-4)+(8×3-4)+(8×4-4)+... +(8×100-4)=8×(1+2+3+4+... +100)-100×4=40000$,所以前100个几何体中只有2个面涂色的小正方体的个数的和为40000.

答案：
(1)4 20
(2)解:观察图形可知,题图①中,只有2个面涂色的小正方体共有4个;题图②中,只有2个面涂色的小正方体共有12个;题图③中,只有2个面涂色的小正方体共有20个.4,12,20 都是4的倍数,可分别写成$4×1,4×3,4×5$的形式,因此第n个图中只有2个面涂色的小正方体的个数是$4(2n-1)=8n-4$,则第100个几何体中只有2个面涂色的小正方体的个数是$8×100-4=796.$
(3)解:根据题意,得$(8×1-4)+(8×2-4)+(8×3-4)+(8×4-4)+... +(8×100-4)=8×(1+2+3+4+... +100)-100×4=40000$,所以前100个几何体中只有2个面涂色的小正方体的个数的和为40000.