1. 如图,已知$∠COD在∠AOB$内部转动,$OE,OF分别平分∠AOC和∠BOD$,则$∠EOF,∠AOB和∠COD$之间的数量关系为
∠EOF=$\frac{1}{2}$(∠AOB+∠COD)
.
答案:
∠EOF=$\frac{1}{2}$(∠AOB+∠COD)
2. 如图,点$A,O,B$在一条直线上,射线$OP从OA$出发,绕点$O$顺时针旋转,同时射线$OQ也以相同的速度从OB$出发,绕点$O$逆时针旋转,当$OP,OQ分别到达OB,OA$上时,运动停止.已知$OM,ON分别平分∠AOP和∠BOQ$,设$∠MON= x^{\circ },∠POQ= y^{\circ }$,则$x与y$之间的数量关系为____.
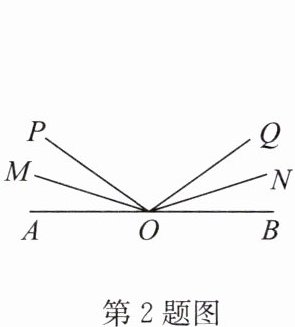

2x−y=180或y=−$\frac{1}{2}$x+90
答案:
2x−y=180或y=−$\frac{1}{2}$x+90 点拨:①如答图①,根据题意,得∠POM+∠QON=x°−y°,
因为OM,ON分别平分∠AOP和∠BOQ,
所以2(x°−y°)=∠AOP+∠BOQ=180°−y°,
所以2x−y=180.
②如答图②,∠POM+∠QON=x°+y°,
因为OM,ON分别平分∠AOP和∠BOQ,
所以x°+y°=180°−y°,所以y=−$\frac{1}{2}$x+90.
因为OM,ON分别平分∠AOP和∠BOQ,
所以2(x°−y°)=∠AOP+∠BOQ=180°−y°,
所以2x−y=180.
②如答图②,∠POM+∠QON=x°+y°,
因为OM,ON分别平分∠AOP和∠BOQ,
所以x°+y°=180°−y°,所以y=−$\frac{1}{2}$x+90.
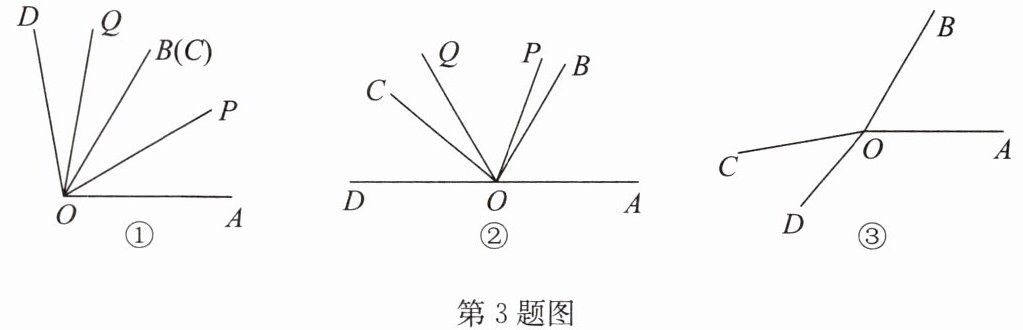
3. 已知$∠AOB和∠COD$均为锐角,$∠AOB>∠COD,OP平分∠AOC,OQ平分∠BOD$,将$∠COD绕点O$逆时针旋转,使$∠BOC= α(0^{\circ }≤α<180^{\circ }).$
(1)若$∠AOB= 60^{\circ },∠COD= 40^{\circ }.$
①当$α=0^{\circ }$时,如图①,则$∠POQ= $____;
②当$α=80^{\circ }$时,如图②,求$∠POQ$的度数;
③当$α=130^{\circ }$时,如图③,请先补全图形,然后求出$∠POQ$的度数.
(2)若$∠AOB= m^{\circ },∠COD= n^{\circ },m>n$,则$∠POQ= $____.(用含$m,n$的代数式表示)
(1)若$∠AOB= 60^{\circ },∠COD= 40^{\circ }.$
①当$α=0^{\circ }$时,如图①,则$∠POQ= $____;
②当$α=80^{\circ }$时,如图②,求$∠POQ$的度数;
③当$α=130^{\circ }$时,如图③,请先补全图形,然后求出$∠POQ$的度数.
(2)若$∠AOB= m^{\circ },∠COD= n^{\circ },m>n$,则$∠POQ= $____.(用含$m,n$的代数式表示)

答案:
解:
(1)①50°
②解:因为∠AOB=60°,∠BOC=α=80°,
所以∠AOC=140°.
因为OP平分∠AOC,所以∠POC=$\frac{1}{2}$∠AOC=70°.
因为∠COD=40°,∠BOC=α=80°,所以∠BOD=120°.因为OQ平分∠BOD,所以∠DOQ=$\frac{1}{2}$∠BOD=60°,所以∠COQ=∠DOQ−∠DOC=20°,
所以∠POQ=∠POC−∠COQ=70°−20°=50°.
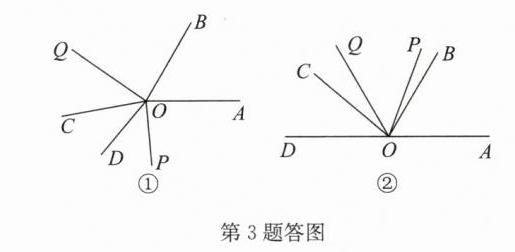
③解:补全图形如答图①.
因为∠AOB=60°,∠BOC=α=130°,
所以∠AOC=360°−60°−130°=170°.
因为OP平分∠AOC,所以∠POC=$\frac{1}{2}$∠AOC=85°.
因为∠COD=40°,∠BOC=α=130°,
所以∠BOD=40°+130°=170°.
因为OQ平分∠BOD,所以∠DOQ=$\frac{1}{2}$∠BOD=85°,所以∠COQ=∠DOQ−∠DOC=85°−40°=45°,
所以∠POQ=∠POC+∠COQ=85°+45°=130°.
(2)$\frac{1}{2}$m°+$\frac{1}{2}$n°或180°−$\frac{1}{2}$m°−$\frac{1}{2}$n°
点拨:当0°≤α≤80°时,如答图②,
因为∠AOB=m°,∠COD=n°,所以∠AOC=m°+α.
因为OP平分∠AOC,所以∠POC=$\frac{1}{2}$(m°+α).
同理可得∠DOQ=$\frac{1}{2}$(n°+α),
所以∠COQ=∠DOQ−∠DOC=$\frac{1}{2}$(n°+α)−n°=$\frac{1}{2}$(−n°+α),所以∠POQ=∠POC−∠COQ=$\frac{1}{2}$(m°+α)−$\frac{1}{2}$(−n°+α)=$\frac{1}{2}$m°+$\frac{1}{2}$n°.
当80°<α<180°时,如答图①,
因为∠AOB=m°,∠BOC=α,
所以∠AOC=360°−m°−α.因为OP平分∠AOC,
所以∠POC=$\frac{1}{2}$∠AOC=180°−$\frac{1}{2}$(m°+α).
因为∠COD=n°,∠BOC=α,且OQ平分∠BOD,
可得∠DOQ=$\frac{1}{2}$(n°+α),
所以∠COQ=∠DOQ−∠DOC=$\frac{1}{2}$(n°+α)−n°=$\frac{1}{2}$(−n°+α),所以∠POQ=∠POC+∠COQ=180°−$\frac{1}{2}$(m°+α)+$\frac{1}{2}$(−n°+α)=180°−$\frac{1}{2}$m°−$\frac{1}{2}$n°.
综上所述,若∠AOB=m°,∠COD=n°,则∠POQ的度数为$\frac{1}{2}$m°+$\frac{1}{2}$n°或180°−$\frac{1}{2}$m°−$\frac{1}{2}$n°.
解:
(1)①50°
②解:因为∠AOB=60°,∠BOC=α=80°,
所以∠AOC=140°.
因为OP平分∠AOC,所以∠POC=$\frac{1}{2}$∠AOC=70°.
因为∠COD=40°,∠BOC=α=80°,所以∠BOD=120°.因为OQ平分∠BOD,所以∠DOQ=$\frac{1}{2}$∠BOD=60°,所以∠COQ=∠DOQ−∠DOC=20°,
所以∠POQ=∠POC−∠COQ=70°−20°=50°.
③解:补全图形如答图①.
因为∠AOB=60°,∠BOC=α=130°,
所以∠AOC=360°−60°−130°=170°.
因为OP平分∠AOC,所以∠POC=$\frac{1}{2}$∠AOC=85°.
因为∠COD=40°,∠BOC=α=130°,
所以∠BOD=40°+130°=170°.
因为OQ平分∠BOD,所以∠DOQ=$\frac{1}{2}$∠BOD=85°,所以∠COQ=∠DOQ−∠DOC=85°−40°=45°,
所以∠POQ=∠POC+∠COQ=85°+45°=130°.
(2)$\frac{1}{2}$m°+$\frac{1}{2}$n°或180°−$\frac{1}{2}$m°−$\frac{1}{2}$n°
点拨:当0°≤α≤80°时,如答图②,
因为∠AOB=m°,∠COD=n°,所以∠AOC=m°+α.
因为OP平分∠AOC,所以∠POC=$\frac{1}{2}$(m°+α).
同理可得∠DOQ=$\frac{1}{2}$(n°+α),
所以∠COQ=∠DOQ−∠DOC=$\frac{1}{2}$(n°+α)−n°=$\frac{1}{2}$(−n°+α),所以∠POQ=∠POC−∠COQ=$\frac{1}{2}$(m°+α)−$\frac{1}{2}$(−n°+α)=$\frac{1}{2}$m°+$\frac{1}{2}$n°.
当80°<α<180°时,如答图①,
因为∠AOB=m°,∠BOC=α,
所以∠AOC=360°−m°−α.因为OP平分∠AOC,
所以∠POC=$\frac{1}{2}$∠AOC=180°−$\frac{1}{2}$(m°+α).
因为∠COD=n°,∠BOC=α,且OQ平分∠BOD,
可得∠DOQ=$\frac{1}{2}$(n°+α),
所以∠COQ=∠DOQ−∠DOC=$\frac{1}{2}$(n°+α)−n°=$\frac{1}{2}$(−n°+α),所以∠POQ=∠POC+∠COQ=180°−$\frac{1}{2}$(m°+α)+$\frac{1}{2}$(−n°+α)=180°−$\frac{1}{2}$m°−$\frac{1}{2}$n°.
综上所述,若∠AOB=m°,∠COD=n°,则∠POQ的度数为$\frac{1}{2}$m°+$\frac{1}{2}$n°或180°−$\frac{1}{2}$m°−$\frac{1}{2}$n°.

查看更多完整答案,请扫码查看


