1. 如图,D 是直径为 10 的$\odot O$中一点,若 OD 长为 3,则过点 D 的所有弦中,最长弦与最短弦的长度差为(
A.2
B.6
C.14
D.18
A
)A.2
B.6
C.14
D.18
答案:
A点拨:如答图,过点D作AB⊥OD,连接OB,则BD=AD=$\frac{1}{2}$AB,∠ODB=90°,
∴BD=$\sqrt{OB^2 - OD^2}=\sqrt{5^2 - 3^2}=4$,
∴AB=2BD=8.
∵过点D的所有弦中,最长弦是直径,
∴最长弦与最短弦的长度差为10−8=2,故选A
∴BD=$\sqrt{OB^2 - OD^2}=\sqrt{5^2 - 3^2}=4$,
∴AB=2BD=8.
∵过点D的所有弦中,最长弦是直径,
∴最长弦与最短弦的长度差为10−8=2,故选A
2. 已知在平面直角坐标系内有一直线$l:(2m+1)x+(m+1)y= 7m+4.$
(1)若不论 m 为何值,直线 l 都经过一定点,求这个定点的坐标;
(2)若以$A(1,2)$为圆心,3 为半径画$\odot A$,求$\odot A$被直线 l 截得的最短弦长.
(1)若不论 m 为何值,直线 l 都经过一定点,求这个定点的坐标;
(2)若以$A(1,2)$为圆心,3 为半径画$\odot A$,求$\odot A$被直线 l 截得的最短弦长.
答案:
(1)直线l:(2m+1)x+(m+1)y=7m+4即m(2x+y−7)+(x+y−4)=0.根据m的任意性可得$\begin{cases}2x + y - 7 = 0 \\x + y - 4 = 0\end{cases}$,解得$\begin{cases}x = 3 \\y = 1\end{cases}$.
∴不论m为何值,直线l都经过定点(3,1).
(2)设定点为P(3,1),则当经过点P的直线l⊥AP时,⊙A被直线l截得的弦最短,如答图.
∵A(1,2),P(3,1),
∴AP=$\sqrt{(1 - 3)^2 + (2 - 1)^2}=\sqrt{5}$.
∵AC=3,
∴PC=$\sqrt{AC^2 - AP^2}=2$,
∴BC=2PC=4,
∴⊙A被直线l截得的最短弦长为4.
(1)直线l:(2m+1)x+(m+1)y=7m+4即m(2x+y−7)+(x+y−4)=0.根据m的任意性可得$\begin{cases}2x + y - 7 = 0 \\x + y - 4 = 0\end{cases}$,解得$\begin{cases}x = 3 \\y = 1\end{cases}$.
∴不论m为何值,直线l都经过定点(3,1).
(2)设定点为P(3,1),则当经过点P的直线l⊥AP时,⊙A被直线l截得的弦最短,如答图.
∵A(1,2),P(3,1),
∴AP=$\sqrt{(1 - 3)^2 + (2 - 1)^2}=\sqrt{5}$.
∵AC=3,
∴PC=$\sqrt{AC^2 - AP^2}=2$,
∴BC=2PC=4,
∴⊙A被直线l截得的最短弦长为4.
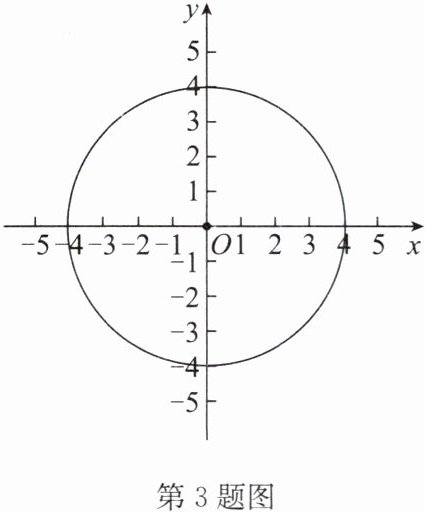
3. 对于$\odot C和\odot C$内一点 P(点 P 与点 C 不重合),给出如下定义:过点 P 可以作出无数条$\odot C$的弦.若在这些弦中,长度为正整数的弦有 k 条,则称点 P 为$\odot C$的 k 属相关点,k 为点 P 关于$\odot C$的相关系数.如图,在平面直角坐标系 xOy 中,已知$\odot O$的半径为 4.
(1)当点 A 的坐标为$(3,0)$时.
①经过点 A 的$\odot O$的所有弦中,最短的弦长为
②点 A 关于$\odot O$的相关系数为
(2)已知点$D(4,3)$,点 B 为$\odot O$的 4 属相关点,求线段 DB 的取值范围.
(1)当点 A 的坐标为$(3,0)$时.
①经过点 A 的$\odot O$的所有弦中,最短的弦长为
$2\sqrt{7}$
;②点 A 关于$\odot O$的相关系数为
5
.(2)已知点$D(4,3)$,点 B 为$\odot O$的 4 属相关点,求线段 DB 的取值范围.
解:∵点B为⊙O的4属相关点,∴经过点B的⊙O的所有弦中,长度为正整数的弦有4条,分别为最长的弦长为8,长度为7的弦有两条,最短的弦长为6.设最短的弦为CQ,则CQ与OB垂直,且QB=CB=3,如答图②,连接OC,∴OB=$\sqrt{OC^2 - BC^2}=\sqrt{4^2 - 3^2}=\sqrt{7}$,∴点B的轨迹是以点O为圆心,$\sqrt{7}$为半径的圆∵D(4,3),∴OD=$\sqrt{3^2 + 4^2}=5$,∴BD的最小值为OD−OB=5 - $\sqrt{7}$,BD的最大值为OD + OB=5 + $\sqrt{7}$,∴线段DB的取值范围为5 - $\sqrt{7}$≤BD≤5 + $\sqrt{7}$

答案:
(1)①$2\sqrt{7}$ ②5 点拨:①如答图①,过点A作MN⊥OA,交⊙O于点M,N,则弦MN为过点A的⊙O的所有弦中最短的弦,连接OM,则OM=4.
∵点A的坐标为(3,0),
∴OA=3.
∵OA⊥MN,
∴MA=NA=$\frac{1}{2}$MN.
∵AM=$\sqrt{OM^2 - OA^2}=\sqrt{4^2 - 3^2}=\sqrt{7}$,
∴MN=2AM=$2\sqrt{7}$.②
∵⊙O的半径为4,
∴⊙O的直径为8,
∴经过点A的⊙O的所有弦中,最长的弦长为8.由①知,经过点A的⊙O的所有弦中,最短的弦长为$2\sqrt{7}$.
∵5<$2\sqrt{7}$<6,
∴经过点A的⊙O的所有弦中,长度为正整数的弦长为8,7,6,由圆的对称性可知:长度为7,6的弦各有两条,
∴经过点A的⊙O的所有弦中,长度为正整数的弦有5条,
∴点A关于⊙O的相关系数为5.
(2)解:
∵点B为⊙O的4属相关点,
∴经过点B的⊙O的所有弦中,长度为正整数的弦有4条,分别为最长的弦长为8,长度为7的弦有两条,最短的弦长为6.设最短的弦为CQ,则CQ与OB垂直,且QB=CB=3,如答图②,连接OC,
∴OB=$\sqrt{OC^2 - BC^2}=\sqrt{4^2 - 3^2}=\sqrt{7}$,
∴点B的轨迹是以点O为圆心,$\sqrt{7}$为半径的圆
∵D(4,3),
∴OD=$\sqrt{3^2 + 4^2}=5$,
∴BD的最小值为OD−OB=5 - $\sqrt{7}$,BD的最大值为OD + OB=5 + $\sqrt{7}$,
∴线段DB的取值范围为5 - $\sqrt{7}$≤BD≤5 + $\sqrt{7}$
(1)①$2\sqrt{7}$ ②5 点拨:①如答图①,过点A作MN⊥OA,交⊙O于点M,N,则弦MN为过点A的⊙O的所有弦中最短的弦,连接OM,则OM=4.
∵点A的坐标为(3,0),
∴OA=3.
∵OA⊥MN,
∴MA=NA=$\frac{1}{2}$MN.
∵AM=$\sqrt{OM^2 - OA^2}=\sqrt{4^2 - 3^2}=\sqrt{7}$,
∴MN=2AM=$2\sqrt{7}$.②
∵⊙O的半径为4,
∴⊙O的直径为8,
∴经过点A的⊙O的所有弦中,最长的弦长为8.由①知,经过点A的⊙O的所有弦中,最短的弦长为$2\sqrt{7}$.
∵5<$2\sqrt{7}$<6,
∴经过点A的⊙O的所有弦中,长度为正整数的弦长为8,7,6,由圆的对称性可知:长度为7,6的弦各有两条,
∴经过点A的⊙O的所有弦中,长度为正整数的弦有5条,
∴点A关于⊙O的相关系数为5.
(2)解:
∵点B为⊙O的4属相关点,
∴经过点B的⊙O的所有弦中,长度为正整数的弦有4条,分别为最长的弦长为8,长度为7的弦有两条,最短的弦长为6.设最短的弦为CQ,则CQ与OB垂直,且QB=CB=3,如答图②,连接OC,
∴OB=$\sqrt{OC^2 - BC^2}=\sqrt{4^2 - 3^2}=\sqrt{7}$,
∴点B的轨迹是以点O为圆心,$\sqrt{7}$为半径的圆
∵D(4,3),
∴OD=$\sqrt{3^2 + 4^2}=5$,
∴BD的最小值为OD−OB=5 - $\sqrt{7}$,BD的最大值为OD + OB=5 + $\sqrt{7}$,
∴线段DB的取值范围为5 - $\sqrt{7}$≤BD≤5 + $\sqrt{7}$
查看更多完整答案,请扫码查看


