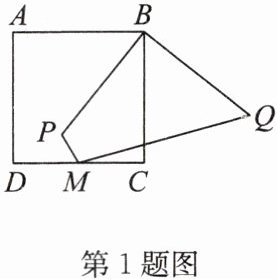
1. (2024·玄武区月考)如图,M是正方形ABCD边CD的中点,P是正方形内一点,连接BP,将线段BP以点B为中心逆时针旋转90°得到线段BQ,连接MP,MQ.若AB = 4√2,MP = √2,则MQ的最小值为______.

答案:
$4\sqrt{5}-\sqrt{2}$ 点拨:连接BM,将△BCM绕点B逆时针旋转$90^{\circ}$得△BEF,连接MF,QF,如答图.
∵∠CBE=$90^{\circ}$,∠ABC=$90^{\circ}$,
∴∠ABC+∠CBE=$180^{\circ}$,
∴A,B,E三点共线.
由旋转性质得PB=QB,MB=FB,
∵∠PBM=∠PBQ - ∠MBQ=$90^{\circ}$ - ∠MBQ=∠FBQ,
∴△BPM≌△BQF(SAS),
∴MP=QF=$\sqrt{2}$,
∴点Q的运动轨迹是以点F为圆心,$\sqrt{2}$为半径的弧.
∵BC=AP=$4\sqrt{2}$,CM=$\frac{1}{2}$CD=$2\sqrt{2}$,
∴BM=$\sqrt{BC^{2}+CM^{2}}=2\sqrt{10}$.
∵∠MBF=$90^{\circ}$,BM=BF,
∴MF=$\sqrt{2}$BM=$\sqrt{2}×2\sqrt{10}=4\sqrt{5}$.
∵MQ≥MF - QF,
∴MQ≥$4\sqrt{5}-\sqrt{2}$,
∴MQ的最小值为$4\sqrt{5}-\sqrt{2}$.

$4\sqrt{5}-\sqrt{2}$ 点拨:连接BM,将△BCM绕点B逆时针旋转$90^{\circ}$得△BEF,连接MF,QF,如答图.
∵∠CBE=$90^{\circ}$,∠ABC=$90^{\circ}$,
∴∠ABC+∠CBE=$180^{\circ}$,
∴A,B,E三点共线.
由旋转性质得PB=QB,MB=FB,
∵∠PBM=∠PBQ - ∠MBQ=$90^{\circ}$ - ∠MBQ=∠FBQ,
∴△BPM≌△BQF(SAS),
∴MP=QF=$\sqrt{2}$,
∴点Q的运动轨迹是以点F为圆心,$\sqrt{2}$为半径的弧.
∵BC=AP=$4\sqrt{2}$,CM=$\frac{1}{2}$CD=$2\sqrt{2}$,
∴BM=$\sqrt{BC^{2}+CM^{2}}=2\sqrt{10}$.
∵∠MBF=$90^{\circ}$,BM=BF,
∴MF=$\sqrt{2}$BM=$\sqrt{2}×2\sqrt{10}=4\sqrt{5}$.
∵MQ≥MF - QF,
∴MQ≥$4\sqrt{5}-\sqrt{2}$,
∴MQ的最小值为$4\sqrt{5}-\sqrt{2}$.

2. (2024·郸城模拟)已知在Rt△ABC中,∠BAC = 90°,AB = AC = √3 + 1.现将△ABC以点B为旋转中心旋转30°,得到△A'BC',直线C'A'交直线AC于点D,则CD的长度为
2或$2\sqrt{3}$
.
答案:
2或$2\sqrt{3}$ 点拨:以点B为旋转中心顺时针旋转$30^{\circ}$时,如答图①,连接BD,过点D作DE⊥BC于点E.
由题意可得,$BA'=BA=\sqrt{3}+1$,$BC=\sqrt{6}+\sqrt{2}$,∠C=$45^{\circ}$,
∴△DEC是等腰直角三角形,DE=CE.
∵BA'=BA=$\sqrt{3}+1$,BD=BD,
∴Rt△ABD≌Rt△A'BD(HL),
∴∠DBA'=∠DBA=$15^{\circ}$,
∴∠DBE=$30^{\circ}$.
设CE=x,则DE=x,BE=$\sqrt{3}x$.
∴$x+\sqrt{3}x=\sqrt{6}+\sqrt{2}$,
∴x=$\sqrt{2}$,
∴CD=$\sqrt{2}x=2$.
以点B为旋转中心逆时针旋转$30^{\circ}$时,如答图②,连接BD,过点D作DE⊥BC于点E,同理可得CE=$\sqrt{6}$,
∴CD=$\sqrt{2}CE=2\sqrt{3}$.
综上所述,CD的长为2或$2\sqrt{3}$.
由题意可得,$BA'=BA=\sqrt{3}+1$,$BC=\sqrt{6}+\sqrt{2}$,∠C=$45^{\circ}$,
∴△DEC是等腰直角三角形,DE=CE.
∵BA'=BA=$\sqrt{3}+1$,BD=BD,
∴Rt△ABD≌Rt△A'BD(HL),
∴∠DBA'=∠DBA=$15^{\circ}$,
∴∠DBE=$30^{\circ}$.
设CE=x,则DE=x,BE=$\sqrt{3}x$.
∴$x+\sqrt{3}x=\sqrt{6}+\sqrt{2}$,
∴x=$\sqrt{2}$,
∴CD=$\sqrt{2}x=2$.
以点B为旋转中心逆时针旋转$30^{\circ}$时,如答图②,连接BD,过点D作DE⊥BC于点E,同理可得CE=$\sqrt{6}$,
∴CD=$\sqrt{2}CE=2\sqrt{3}$.
综上所述,CD的长为2或$2\sqrt{3}$.
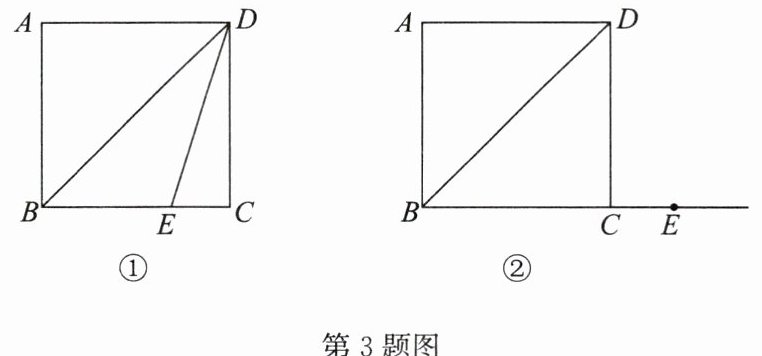
3. 在正方形ABCD中,点E在射线BC上(不与点B,C重合),连接DB,DE,将DE绕点E逆时针旋转90°得到EF,连接BF.
(1)如图①,点E在BC边上.
①依题意补全图形;
②若AB = 6,EC = 2,求BF的长.
(2)如图②,点E在BC边的延长线上,用等式表示线段BD,BE,BF之间的数量关系.
(1)如图①,点E在BC边上.
①依题意补全图形;
②若AB = 6,EC = 2,求BF的长.
(2)如图②,点E在BC边的延长线上,用等式表示线段BD,BE,BF之间的数量关系.

答案:
解:
(1)①补全图形如答图①所示.
②过点F作FH⊥CB,交CB的延长线于点H,则∠H=$90^{\circ}$.
∵DE绕点E逆时针旋转$90^{\circ}$得到EF,
∴DE=EF,∠DEF=$90^{\circ}$.
∵四边形ABCD是正方形,
∴CD=AB=BC=6,∠C=$90^{\circ}$.
∵∠DEF=∠C=$90^{\circ}$,
∴∠DEC+∠FEH=$90^{\circ}$,∠DEC+∠EDC=$90^{\circ}$,
∴∠FEH=∠EDC.
在△EFH和△DEC中,$\begin{cases} ∠H=∠C=90^{\circ}, \\ ∠FEH=∠EDC, \\ EF=ED, \end{cases}$
∴△EFH≌△DEC(AAS),
∴EC=FH=2,CD=BC=EH=6,
∴HB=EC=2.
在Rt△FHB中,BF=$\sqrt{FH^{2}+BH^{2}}=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$.
(2)如答图②,过点F作FH⊥BC,交BC于点H,则∠FHE=$90^{\circ}$.
∵DE绕点E逆时针旋转$90^{\circ}$得到EF,
∴DE=EF,∠DEF=$90^{\circ}$.
∵四边形ABCD是正方形,
∴CD=BC,∠DCB=$90^{\circ}$,
∴∠DCE=$90^{\circ}$.
∵∠DEF=∠DCE=$90^{\circ}$,
∴∠DEC+∠FEH=$90^{\circ}$,∠DEC+∠EDC=$90^{\circ}$,
∴∠FEH=∠EDC.
在△EFH和△DEC中,$\begin{cases} ∠FHE=∠DCE=90^{\circ}, \\ ∠FEH=∠EDC, \\ EF=ED, \end{cases}$
∴△EFH≌△DEC(AAS),
∴EC=FH,CD=BC=EH,
∴HB=EC=HF,
∴△DCB和△BHF都是等腰直角三角形,
∴BD=$\sqrt{2}$BC=$\sqrt{2}$HE,BF=$\sqrt{2}$BH,
∵HE+BH=BE,
∴BD+BF=$\sqrt{2}$BE.

解:
(1)①补全图形如答图①所示.
②过点F作FH⊥CB,交CB的延长线于点H,则∠H=$90^{\circ}$.
∵DE绕点E逆时针旋转$90^{\circ}$得到EF,
∴DE=EF,∠DEF=$90^{\circ}$.
∵四边形ABCD是正方形,
∴CD=AB=BC=6,∠C=$90^{\circ}$.
∵∠DEF=∠C=$90^{\circ}$,
∴∠DEC+∠FEH=$90^{\circ}$,∠DEC+∠EDC=$90^{\circ}$,
∴∠FEH=∠EDC.
在△EFH和△DEC中,$\begin{cases} ∠H=∠C=90^{\circ}, \\ ∠FEH=∠EDC, \\ EF=ED, \end{cases}$
∴△EFH≌△DEC(AAS),
∴EC=FH=2,CD=BC=EH=6,
∴HB=EC=2.
在Rt△FHB中,BF=$\sqrt{FH^{2}+BH^{2}}=\sqrt{2^{2}+2^{2}}=2\sqrt{2}$.
(2)如答图②,过点F作FH⊥BC,交BC于点H,则∠FHE=$90^{\circ}$.
∵DE绕点E逆时针旋转$90^{\circ}$得到EF,
∴DE=EF,∠DEF=$90^{\circ}$.
∵四边形ABCD是正方形,
∴CD=BC,∠DCB=$90^{\circ}$,
∴∠DCE=$90^{\circ}$.
∵∠DEF=∠DCE=$90^{\circ}$,
∴∠DEC+∠FEH=$90^{\circ}$,∠DEC+∠EDC=$90^{\circ}$,
∴∠FEH=∠EDC.
在△EFH和△DEC中,$\begin{cases} ∠FHE=∠DCE=90^{\circ}, \\ ∠FEH=∠EDC, \\ EF=ED, \end{cases}$
∴△EFH≌△DEC(AAS),
∴EC=FH,CD=BC=EH,
∴HB=EC=HF,
∴△DCB和△BHF都是等腰直角三角形,
∴BD=$\sqrt{2}$BC=$\sqrt{2}$HE,BF=$\sqrt{2}$BH,
∵HE+BH=BE,
∴BD+BF=$\sqrt{2}$BE.

查看更多完整答案,请扫码查看


