1. 我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记$p= \frac {a+b+c}{2}$,则其面积$S= \sqrt {p(p-a)(p-b)(p-c)}$。这个公式也被称为海伦—秦九韶公式。若$p= 5$,$c= 4$,则此三角形面积的最大值为(
A.$\sqrt {5}$
B.4
C.$2\sqrt {5}$
D.5
C
)A.$\sqrt {5}$
B.4
C.$2\sqrt {5}$
D.5
答案:
C 点拨:
∵p=(a+b+c)/2,p=5,c=4,
∴5=(a+b+4)/2,
∴a+b=6,
∴a=6-b,
∴S=√[p(p-a)(p-b)(p-c)]=√[5(5-a)(5-b)(5-4)]=√[5(5-a)(5-b)]=√[5(5-(6-b))(5-b)]=√(-5b²+30b-25)=√[-5(b-3)²+20],
∴当b=3时,S取得最大值√20=2√5.
∵p=(a+b+c)/2,p=5,c=4,
∴5=(a+b+4)/2,
∴a+b=6,
∴a=6-b,
∴S=√[p(p-a)(p-b)(p-c)]=√[5(5-a)(5-b)(5-4)]=√[5(5-a)(5-b)]=√[5(5-(6-b))(5-b)]=√(-5b²+30b-25)=√[-5(b-3)²+20],
∴当b=3时,S取得最大值√20=2√5.
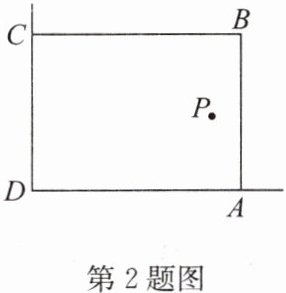
2. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设$AB= xm$,花园面积为$Sm^{2}$。
(1)若花园的面积为$252m^{2}$,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值。
(1)若花园的面积为$252m^{2}$,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值。

答案:
(1)由AB=x m,可知BC=(32-x)m,根据题意得x(32-x)=252.解这个方程得x₁=18,x₂=14.答:x的值为18或14.
(2)根据题意得S=x(32-x)=-(x-16)²+256.
∵在P处有一棵树与墙CD,AD的距离分别是17 m和6 m,
∴6≤x≤15,
∴当x=15时,S取得最大值,S最大=-(15-16)²+256=255.答:花园面积的最大值是255 m².
(1)由AB=x m,可知BC=(32-x)m,根据题意得x(32-x)=252.解这个方程得x₁=18,x₂=14.答:x的值为18或14.
(2)根据题意得S=x(32-x)=-(x-16)²+256.
∵在P处有一棵树与墙CD,AD的距离分别是17 m和6 m,
∴6≤x≤15,
∴当x=15时,S取得最大值,S最大=-(15-16)²+256=255.答:花园面积的最大值是255 m².
查看更多完整答案,请扫码查看


