《2025年启东中学作业本九年级数学上册人教版》

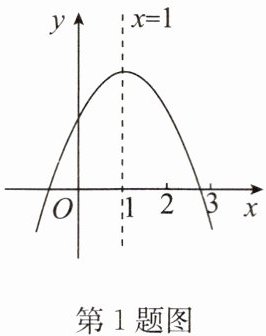
1. (2024·禹城期末)如图,抛物线$y= ax^{2}+bx+c的对称轴是直线x= 1$,则以下五个结论：①$abc＞0$,②$2a+b= 0$,③$b^{2}＞4ac$,④$4a+2b+c＞0$,⑤$3a+c＜0$中,正确的有(D)

A.1 个
B.2 个
C.3 个
D.4 个

答案： D 点拨:
∵图象开口向下,
∴a＜0.
∵图象交y轴于正半轴,
∴c＞0.
∵对称轴是直线x=1,
∴$-\dfrac{b}{2a}=1,$
∴b=-2a,
∴b＞0,
∴abc＜0,故①错;
∵b=-2a,
∴b+2a=0,故②对;
∵图象与x轴有两个交点,
∴Δ=b²-4ac＞0,即b²＞4ac,故③对;
根据图象可知,点(-1,0)关于直线x=1对称的点为(3,0),
故图象与x轴的交点在-1和3之间,且开口向下,
∴x=2时,y=4a+2b+c＞0,故④对;
由图象知:x=-1时,y=a-b+c＜0.
∵b=-2a,
∴a-(-2a)+c＜0,即3a+c＜0,故⑤对.
故选D.

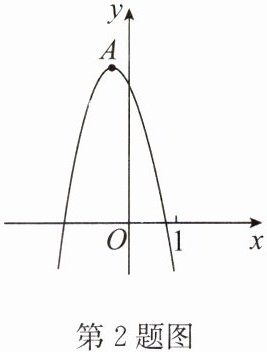
2. (2024·德阳)如图,抛物线$y= ax^{2}+bx+c$的顶点 A 的坐标为$(-\frac {1}{3},n)$,与 x 轴的一个交点位于 0 和 1 之间,则以下结论：①$abc＞0$；②$5b+2c＜0$；③若抛物线经过点$(-6,y_{1}),(5,y_{2})$,则$y_{1}＞y_{2}$；④若关于 x 的一元二次方程$ax^{2}+bx+c= 4$无实数根,则$n＜4$.其中正确的结论是______①②④(填序号).

答案： ①②④ 点拨:
∵抛物线y=ax²+bx+c的顶点A的坐标为$(-\dfrac{1}{3},n),$
∴$-\dfrac{b}{2a}=-\dfrac{1}{3},$
∴$a=\dfrac{3}{2}b.$
∵抛物线开口向下,即a＜0,
∴b＜0,当x=0时,y=c＞0,
∴abc＞0,故①正确.
由图象可得,当x=1时,y=a+b+c＜0,
∴5b+2c＜0,故②正确.
∵直线$x=-\dfrac{1}{3}$是抛物线的对称轴,
∴点(-6,y₁)到对称轴的距离大于点(5,y₂)到对称轴的距离,
∴y₁＜y₂,故③错误.
∵关于x的一元二次方程ax²+bx+c=4无实数根,
∴顶点$A(-\dfrac{1}{3},n)$在直线y=4的下方,
∴n＜4,故④正确.

3. (2023·武汉改编)抛物线$y= ax^{2}+bx+c$(a,b,c 是常数,$c＜0$)经过$(1,1),(m,0),(n,0)$三点,且$n≥3$.给出下列四个结论：
①$b＜0$；②$4ac-b^{2}＜4a$；
③当$n= 3$时,若点$(2,t)$在该抛物线上,则$t＞1$；
④若关于 x 的一元二次方程$ax^{2}+bx+c= x$有两个相等的实数根,则$0\lt m≤\frac {1}{3}$.
写出正确的结论,并说明理由.

答案： 解:正确的结论是②③④.理由如下:
①
∵图象经过点(1,1),c＜0,
∴抛物线与y轴的负半轴有交点,
∵(n,0)中n≥3,
∴抛物线与x轴的一个交点一定在点(3,0)或(3,0)的右侧,
∴抛物线的开口一定向下,即a＜0.
把(1,1)代入y=ax²+bx+c,得a+b+c=1,
即b=1-a-c.
∵a＜0,c＜0,
∴b＞0,故①错误;
②
∵a＜0,b＞0,c＜0,
∴\dfrac{c}{a}＞0,
∴方程ax²+bx+c=0的两个根的积大于0,即mn＞0.
∵n≥3,
∴m＞0,
∴$\dfrac{m+n}{2}＞1.5,$即抛物线的对称轴在直线x=1.5的右侧,
∴抛物线的顶点在点(1,1)的右侧,
∴$\dfrac{4ac-b²}{4a}＞1.$
∵4a＜0,
∴4ac-b²＜4a,故②正确;
③
∵抛物线的对称轴在直线x=1.5的右侧,
∴点(1,1)到对称轴的距离大于点(2,t)到对称轴的距离,
∵a＜0,抛物线开口向下,
∴距离抛物线的对称轴越近,函数值越大,
∴t＞1,故③正确;
④方程ax²+bx+c=x可变形为ax²+(b-1)x+c=0.
∵方程有两个相等的实数根,
∴Δ=(b-1)²-4ac=0,
由①得a+b+c=1,即1-b=a+c,
∴(a+c)²-4ac=0,即a²+2ac+c²-4ac=0,
∴(a-c)²=0,
∴a-c=0,即a=c.
∵点(m,0),(n,0)在抛物线上,
∴m,n为方程ax²+bx+c=0的两个根,
∴$mn=\dfrac{c}{a}=1,$
∴$n=\dfrac{1}{m}.$
∵n≥3,
∴$\dfrac{1}{m}≥3,$
∴0＜m≤\dfrac{1}{3},故④正确.
综上,正确的结论是②③④.