《2025年启东中学作业本九年级数学上册人教版》

1. 在二次函数 $ y = -\frac{1}{12}(x - 2)^2 + 3 $ 的图象上有两点 $ (-1, y_1) $,$ (1, y_2) $,则 $ y_1 - y_2 $ 的值是(A)
A.负数
B.零
C.正数
D.不能确定

答案： A 点拨:
∵二次函数$y=-\frac{1}{12}(x-2)^2+3$,
∴该二次函数的图象开口向下，且对称轴为直线$x=2$.
∵点$(-1,y_1),(1,y_2)$是二次函数$y=-\frac{1}{12}(x-2)^2+3$ 的图象上的两点，且$-1＜1＜2$,
∴两点都在对称轴的左侧，$y$随$x$的增大而增大，
∴$y_1＜y_2$,
∴$y_1 - y_2$的值是负数.故选A

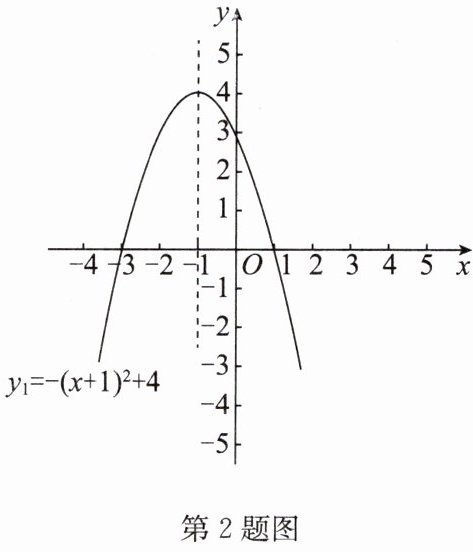
2. (1)已知二次函数 $ y_1 = -(x + 1)^2 + 4 $ 的图象如图所示,请在同一平面直角坐标系中画出二次函数 $ y_2 = -(x - 2)^2 + 1 $ 的图象；
(2)平行于 $ x $ 轴的直线 $ y = k $ 在抛物线 $ y_2 = -(x - 2)^2 + 1 $ 上截得线段 $ AB = 4 $(点 $ A $ 在点 $ B $ 的左侧),求抛物线 $ y_2 = -(x - 2)^2 + 1 $ 的顶点到线段 $ AB $ 的距离；
(3)当 $ -1 ＜ x ＜ 2 $ 时,利用函数图象比较 $ y_1 $ 与 $ y_2 $ 的大小.

答案：
解:
(1)函数的图象如答图所示.
(2)根据题意可设$A(x_1,k),B(x_2,k)$,
∵$AB=4$，且点$A,B$关于抛物线$y_2=-(x-2)^2+1$的对称轴$x=2$对称,
∴$x_1=0,x_2=4$,
∴$k=-3$.
∵抛物线$y_2=-(x-2)^2+1$的顶点坐标为$(2,1)$,
∴抛物线$y_2=-(x-2)^2+1$的顶点到线段$AB$的距离为 4
(3)当$-1＜x＜1$时,$y_1＞y_2$;当$x=1$时,$y_1=y_2$;当$1＜x＜2$时,$y_1＜y_2$.
　　　

3. 在平面直角坐标系中,把函数 $ y = ax^2 + 2bx + 1 $($ a $,$ b $ 为常数)的图象记为 $ G $.
(1)设 $ k \neq 0 $,若点 $ A(3 - k, t) $ 在 $ G $ 上,则点 $ B(3 + k, t) $ 必在 $ G $ 上,且 $ G $ 过点 $ C(4, 9) $,求 $ G $ 的函数解析式；
(2)若点 $ D(1, y_1) $,$ E(4, y_2) $ 是(1)中函数图象上的两点,比较 $ y_1 $ 与 $ y_2 $ 的大小；
(3)若点 $ P(m, y_3) $,$ Q(m + 3, y_4) $ 是(1)中函数图象上的两点,比较 $ y_3 $ 与 $ y_4 $ 的大小.

答案： 解:
(1)
∵$\frac{3 - k + 3 + k}{2}=3$,
∴抛物线的对称轴为直线$x=-\frac{2b}{2a}=-\frac{b}{a}=3$,
∴$b=-3a$.将$(4,9)$代入$y=ax^2 - 6ax + 1$,得
　$9=16a - 24a + 1$,解得$a=-1$.
∴$y=-x^2 + 6x + 1$.
(2)把$x=1,x=4$分别代入抛物线的函数解析式$y=-x^2 + 6x + 1$,得$y_1=6,y_2=9$,
∴$y_1＜y_2$.
(3)
∵抛物线$y=-x^2 + 6x + 1$开口向下,对称轴为直线$x=3$,
∴抛物线上到对称轴距离越远的点对应的$y$值越小,
∴$|m - 3|=|m + 3 - 3|$时,$y_3=y_4$,解得$m=\frac{3}{2}$;
　$|m - 3|＞|m + 3 - 3|$时,$y_3＜y_4$,解得$m＜\frac{3}{2}$;
　$|m - 3|＜|m + 3 - 3|$时,$y_3＞y_4$,解得$m＞\frac{3}{2}$.
　综上所述，当$m=\frac{3}{2}$时,$y_3=y_4$;当$m＜\frac{3}{2}$时,$y_3＜y_4$;当$m＞\frac{3}{2}$时,$y_3＞y_4$.