《2025年启东中学作业本九年级数学上册人教版》

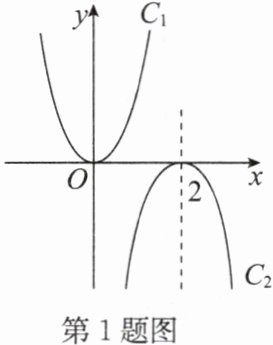
1. (2024·上虞区期末)如图,将抛物线 $C_{1}:y = x^{2}$ 向右平移 2 个单位长度后,再将该图象关于 $x$ 轴进行轴对称变换得到抛物线 $C_{2}:y = ax^{2}+bx + c$。则下列是关于抛物线 $C_{2}$ 的函数解析式的是(A)

A.$y = -x^{2}+4x - 4$
B.$y = -x^{2}-4x - 4$
C.$y = x^{2}+4x - 4$
D.$y = x^{2}-4x - 4$

答案： A

2. 将抛物线 $y = -x^{2}+2x + 3$ 在 $x$ 轴下方的部分沿 $x$ 轴翻折到 $x$ 轴上方,图象的其余部分不变,得到一个新图象,若直线 $y = x + b$ 与这个新图象有 2 个公共点,求 $b$ 的取值范围。

答案： 解:
∵将抛物线 y=-x²+2x+3=-(x-1)²+4 在x轴下方的部分沿x轴翻折到x轴上方，
∴翻折上来的部分的图象的函数解析式为 y=(x-1)²-4=x²-2x-3,
∴新图象的函数解析式为y={-x²+2x+3(-1＜x＜3),x²-2x-3(x≤-1或x≥3).①若直线y=x+b与x轴的交点在点(-1,0),(3,0)之间,则直线与这个新图象有2个公共点，当y=x+b过点(-1,0)时,0=-1+b,解得b=1；当y=x+b过点(3,0)时,3+b=0,解得b=-3，
∴-3＜b＜1.②若直线y=x+b与y=-x²+2x+3没有公共点,则直线与这个新图象有2个公共点,由x+b=-x²+2x+3,得x²-x+b-3=0,则Δ＜0，
∴1+12-4b＜0,
∴b＞13/4.综上所述,b的取值范围是-3＜b＜1或b＞13/4.

3. (2024·镇江期末)如图①,抛物线 $C_{1}$ 与 $x$ 轴的两个交点中的左边的一个交点为 $A(-3,0)$,将该抛物线沿 $y$ 轴翻折,得到抛物线 $C_{2}$,点 $A$ 的对应点为点 $A'$,将抛物线 $C_{1},C_{2}$ 沿 $x$ 轴分别向右、左平移 1 个单位长度后,恰好重合(如图②),重合后的抛物线的顶点为 $(0,4)$。
(1)求平移前的抛物线 $C_{1}$ 对应的二次函数的解析式。
(2)小明发现：将抛物线 $C_{1},C_{2}$ 沿 $x$ 轴分别向右、左平移 $m(m ＞ 0)$ 个单位长度,平移后得到的两条抛物线与 $y$ 轴的交点 $P(0,t)$ 的位置在发生变化。
①试求出 $t$ 与 $m$ 之间的函数解析式；
②在平移过程中,求当 $m$ 为何值时,$\triangle PAA'$ 是等边三角形。

答案：
(1)解:设平移前的抛物线C₁的函数解析式为y=a(x-h)²+k,则沿y轴翻折后的抛物线C₂的函数解析式为y=a(x+h)²+k,
∴平移后的抛物线C₁的函数解析式为y=a(x-h-1)²+k,平移后的抛物线C₂的函数解析式为y=a(x+h+1)²+k.
∵重合后的抛物线的顶点为(0,4),
∴h+1=-h-1=0,k=4,
∴h=-1,k=4，
∴平移前的抛物线C₁的函数解析式为y=a(x+1)²+4.将(-3,0)代入可得4a+4=0,解得a=-1，
∴平移前的抛物线C₁的函数解析式为y=-(x+1)²+4=-x²-2x+3.
(2)①平移后的抛物线C₁的函数解析式为y=-(x+1-m)²+4,平移后的抛物线C₂的函数解析式为y=-(x-1+m)²+4,当x=0时,t=-m²+2m+3.②
∵△PAA'是等边三角形,
∴∠APO=30°.
∵OP=|t|,AO=|3-m|，
∴|3-m|=√3/3|t|=√3/3|-m²+2m+3|，解得m=√3-1或m=3(舍去)或m=-√3-1(舍去).
∴当m=√3-1时,△PAA'是等边三角形.