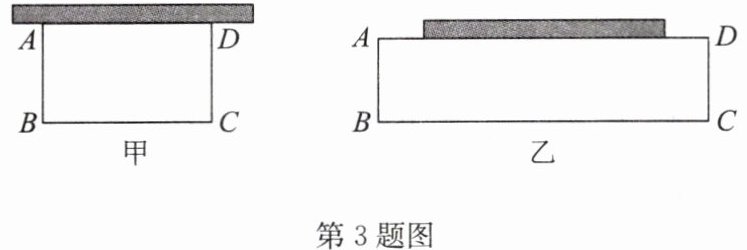
3. 植物园有一块足够大的空地,其中有一堵长为6m的墙,现准备用20m长的篱笆围一个矩形花圃。小俊设计了如图所示的甲和乙两种方案:方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长。
(1)按方案甲围矩形花圃,设BC的长为xm,矩形ABCD的面积为$ym^{2}$。
①求y与x之间的函数关系式;
②求矩形ABCD面积的最大值。
(2)甲、乙哪种方案能使围成的矩形花圃的面积最大?最大面积是多少?
(1)按方案甲围矩形花圃,设BC的长为xm,矩形ABCD的面积为$ym^{2}$。
①求y与x之间的函数关系式;
②求矩形ABCD面积的最大值。
(2)甲、乙哪种方案能使围成的矩形花圃的面积最大?最大面积是多少?

答案:
(1)①根据题意,得AB=(1/2)(20-x)=(10-(1/2)x)m,
∴y=(10-(1/2)x)x=-(1/2)x²+10x,
∵墙长为6 m,
∴0<x≤6,
∴y与x之间的函数关系式为y=-(1/2)x²+10x(0<x≤6).②y=-(1/2)x²+10x=-(1/2)(x-10)²+50,
∵-(1/2)<0,
∴当x<10时,y随x的增大而增大.
∵0<x≤6,
∴当x=6时,y有最大值,最大值为42.答:矩形ABCD面积的最大值为42 m².
(2)乙方案:设BC的长是n m,矩形花圃的面积是S m²,则AB=(1/2)[20-n-(n-6)]=(13-n)m,
∴S=n(13-n)=-(n-(13/2))²+(169/4).
∵13-n>0,
∴n<13,
∵-1<0,6<n<13,
∴当n=13/2时,S有最大值,最大值为169/4.
∵42<169/4,
∴乙方案能使围成的矩形花圃的面积最大,最大面积是169/4 m².
(1)①根据题意,得AB=(1/2)(20-x)=(10-(1/2)x)m,
∴y=(10-(1/2)x)x=-(1/2)x²+10x,
∵墙长为6 m,
∴0<x≤6,
∴y与x之间的函数关系式为y=-(1/2)x²+10x(0<x≤6).②y=-(1/2)x²+10x=-(1/2)(x-10)²+50,
∵-(1/2)<0,
∴当x<10时,y随x的增大而增大.
∵0<x≤6,
∴当x=6时,y有最大值,最大值为42.答:矩形ABCD面积的最大值为42 m².
(2)乙方案:设BC的长是n m,矩形花圃的面积是S m²,则AB=(1/2)[20-n-(n-6)]=(13-n)m,
∴S=n(13-n)=-(n-(13/2))²+(169/4).
∵13-n>0,
∴n<13,
∵-1<0,6<n<13,
∴当n=13/2时,S有最大值,最大值为169/4.
∵42<169/4,
∴乙方案能使围成的矩形花圃的面积最大,最大面积是169/4 m².
1. 东方商厦将进货价为 70 元/件的某种商品按零售价 100 元/件售出时,每天能卖出 20 件,若这种商品的零售价在一定范围内每件每降价 1 元,其日销量就增加 1 件. 为了获取最大日销售利润,则每件商品应降价
5
元.
答案:
5 点拨:设每件商品降价x元,日销售利润为W元,由题意,得W=(100-70-x)(20+x)=-x²+10x+600=-(x-5)²+625,
∵a=-1<0,
∴当x=5时,W取得最大值,
∴每件商品应降价5元.
∵a=-1<0,
∴当x=5时,W取得最大值,
∴每件商品应降价5元.
2. 某商品每件的进价为 20 元,在试销阶段该商品的日销售量 y(件)与商品的日销售单价 x(元)之间的关系为 $ y = \begin{cases} -10x + 400(20 \leq x \leq 30) \\ -4x + 220(30 < x \leq 45) \end{cases} $ (规定该商品的日销售单价不得低于进价且不得高于 45 元). 若日销售单价 x(元)为整数,则当日销售单价 x(元)为
37 或 38
元时,该商品的日销售利润最大,最大利润是1224
元.
答案:
37 或 38 1224 点拨:设日销售利润为w元,当20≤x≤30时,w=(x-20)(-10x+400)=-10x²+600x-8000=-10(x-30)²+1000,
∴当x=30时,w取得最大值,最大值为1000;当30<x≤45时,w=(x-20)(-4x+220)=-4x²+300x-4400=-4(x-37.5)²+1225,
∵x为整数,
∴x=37 或x=38时,w取得最大值,最大值为-4×$\frac{1}{4}$+1225=1224.
∵1000<1224,
∴当日销售单价为37元或38元时,该商品的日销售利润最大,最大利润是1224元.
∴当x=30时,w取得最大值,最大值为1000;当30<x≤45时,w=(x-20)(-4x+220)=-4x²+300x-4400=-4(x-37.5)²+1225,
∵x为整数,
∴x=37 或x=38时,w取得最大值,最大值为-4×$\frac{1}{4}$+1225=1224.
∵1000<1224,
∴当日销售单价为37元或38元时,该商品的日销售利润最大,最大利润是1224元.
查看更多完整答案,请扫码查看


