《2025年启东中学作业本九年级数学上册人教版》

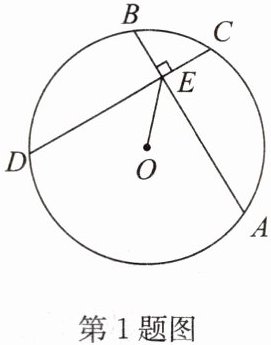
1. 如图,在半径为$\sqrt{7}的\odot O$中,弦$AB\perp弦CD$,垂足为$E$,连接$OE$,若$\angle OEA = 30^{\circ}$,$CE = 1$,则弦$CD$的长为( )


A.$\frac{1}{2}$
B.$1$
C.$2$
D.$4$

答案：
D 点拨:如答图，过点O作OH⊥DC于点H，连接OD，则DH=CH。
设DH=x，则HE=x - 1。
∵弦AB⊥弦CD，
∴∠AED=90°，
∴∠OED=90° - ∠OEA=90° - 30°=60°，
在Rt△OHE中，OH = √3HE = √3(x - 1)，
在Rt△ODH中，x² + [√3(x - 1)]² = (√7)²，
整理得2x² - 3x - 2 = 0，解得x₁ = -1/2(舍去)，x₂ = 2，
∴DH = 2，
∴CD = 2DH = 4。

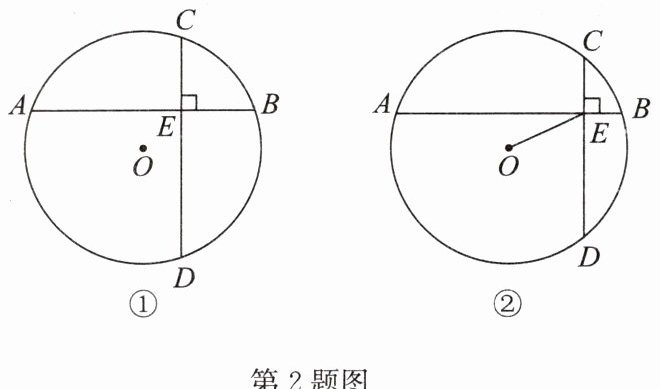
2. 已知在圆$O$中,弦$AB垂直弦CD于点E$。
(1)如图①,若$CE = BE$,求证：$AB = CD$。
(2)如图②,若$AB = 8$,$CD = 6$,$OE = \sqrt{11}$。
①求圆$O$的半径；
②求弓形$CBD$的面积。

答案：

(1)证明:如答图①，连接AD，BC。

∵CE = BE，
∴∠B = ∠C。
∵∠A = ∠C，∠B = ∠D，
∴∠A = ∠D，
∴AE = DE，
∴AB = CD。
(2)解:①如答图②，连接OA，OC，OD，过点O作OM⊥AB于点M，作ON⊥CD于点N。设圆O的半径为r，则AM = 1/2AB = 4，DN = 1/2CD = 3，ME = ON。
∵OM² = OA² - AM² = r² - 4²，ME² = ON² = OD² - DN² = r² - 3²，OM² + ME² = OE²，
∴r² - 4² + r² - 3² = (√11)²，
∴r = 3√2，
∴圆O的半径为3√2。
②
∵DN = 3，OD = 3√2，
∴ON = √[(3√2)² - 3²] = 3，
∴∠D = ∠C = 45°，
∴∠COD = 90°，
∴弓形CBD的面积为(90π×(3√2)²)/360 - 1/2×3√2×3√2 = 9π/2 - 9。