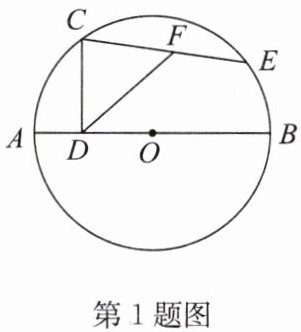
1. 如图,$AB是\odot O$的直径,点$C在\odot O$上,$CD\perp AB$,垂足为$D$,$AD = 2$,点$E是\odot O$上的动点(不与点$C$重合),点$F为CE$的中点,若在点$E运动过程中DF的最大值为4$,则$CD$的值为( )
A.$2\sqrt{3}$
B.$2\sqrt{2}$
C.$3\sqrt{2}$
D.$\frac{7}{2}$

A.$2\sqrt{3}$
B.$2\sqrt{2}$
C.$3\sqrt{2}$
D.$\frac{7}{2}$
答案:
A 点拨:方法一:如答图①,连接OE,OC,取OC的中点M,连接MF和DM.设⊙O的半径为r.
∵点F为CE的中点,
∴MF=$\frac{1}{2}$OE=$\frac{r}{2}$.
∵点E是⊙O上的动点(不与点C重合),点C为顶点,
∴点F的运动轨迹是以点M为圆心,以MF的长为半径的圆,则DF≤DM+MF,
∴当D,M,F三点共线时,DF有最大值4,此时DF=DM+MF,
∴DM=4−$\frac{r}{2}$.
∵CD⊥AB,
∴∠CDO=90°.
∵点M为OC的中点,
∴DM=$\frac{1}{2}$OC=$\frac{r}{2}$,
∴$\frac{r}{2}$=4−$\frac{r}{2}$,解得r=4,
∴OD=OA−AD=2.
在Rt△CDO中,$CD=\sqrt {OC^{2}-OD^{2}}=2\sqrt {3}$.
方法二:如答图②,延长CD交⊙O于点Q,连接QE,CO.
∵CD⊥AB,AB是直径,
∴CD=DQ.
又
∵点F是CE的中点,
∴QE=2DF;
当QE为直径时,DF有最大值,
此时QE=2DF=8,
∴AO=CO=4,
∴DO=2.
在Rt△CDO中,$CD=\sqrt {OC^{2}-OD^{2}}=2\sqrt {3}$.

A 点拨:方法一:如答图①,连接OE,OC,取OC的中点M,连接MF和DM.设⊙O的半径为r.
∵点F为CE的中点,
∴MF=$\frac{1}{2}$OE=$\frac{r}{2}$.
∵点E是⊙O上的动点(不与点C重合),点C为顶点,
∴点F的运动轨迹是以点M为圆心,以MF的长为半径的圆,则DF≤DM+MF,
∴当D,M,F三点共线时,DF有最大值4,此时DF=DM+MF,
∴DM=4−$\frac{r}{2}$.
∵CD⊥AB,
∴∠CDO=90°.
∵点M为OC的中点,
∴DM=$\frac{1}{2}$OC=$\frac{r}{2}$,
∴$\frac{r}{2}$=4−$\frac{r}{2}$,解得r=4,
∴OD=OA−AD=2.
在Rt△CDO中,$CD=\sqrt {OC^{2}-OD^{2}}=2\sqrt {3}$.
方法二:如答图②,延长CD交⊙O于点Q,连接QE,CO.
∵CD⊥AB,AB是直径,
∴CD=DQ.
又
∵点F是CE的中点,
∴QE=2DF;
当QE为直径时,DF有最大值,
此时QE=2DF=8,
∴AO=CO=4,
∴DO=2.
在Rt△CDO中,$CD=\sqrt {OC^{2}-OD^{2}}=2\sqrt {3}$.

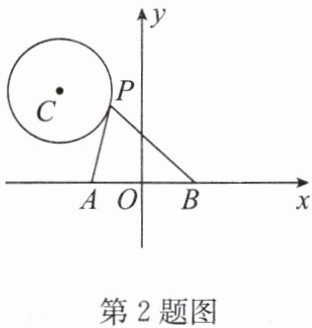
2. 如图,在平面直角坐标系中,点$P是以C(-\sqrt{2},\sqrt{3})$为圆心,$1为半径的\odot C$上的一个动点,已知$A(-1,0)$,$B(1,0)$,连接$PA$,$PB$,则$PA^{2}+PB^{2}$的最小值是______
14−4$\sqrt{5}$
。
答案:
14−4$\sqrt{5}$ 点拨:设P(x,y).
∵PA²=(x+1)²+y²,PB²=(x−1)²+y²,
∴PA²+PB²=2x²+2y²+2=2(x²+y²)+2.
∵OP²=x²+y²,
∴PA²+PB²=2OP²+2,
当点P为OC与圆的交点时,OP取得最小值,
∴OP的最小值为CO−CP=√5−1,
∴PA²+PB²的最小值为14−4√5.
∵PA²=(x+1)²+y²,PB²=(x−1)²+y²,
∴PA²+PB²=2x²+2y²+2=2(x²+y²)+2.
∵OP²=x²+y²,
∴PA²+PB²=2OP²+2,
当点P为OC与圆的交点时,OP取得最小值,
∴OP的最小值为CO−CP=√5−1,
∴PA²+PB²的最小值为14−4√5.
3. 已知直线$l:y= \frac{3}{4}x - 3与x$轴、$y轴分别交于点A$,$B$。
(1) 求$AB$的长;
(2) 如图①,若点$P的坐标是(0,4)$,点$M是直线l$上的一个动点,求$PM$的最短长度;
(3) 如图②,若点$P是以点C(0,1)$为圆心,$1$为半径的圆上一动点,连接$PA$,$PB$。求$\triangle PAB$面积的最小值与最大值之和。

(1) 求$AB$的长;
(2) 如图①,若点$P的坐标是(0,4)$,点$M是直线l$上的一个动点,求$PM$的最短长度;
(3) 如图②,若点$P是以点C(0,1)$为圆心,$1$为半径的圆上一动点,连接$PA$,$PB$。求$\triangle PAB$面积的最小值与最大值之和。

答案:
解:
(1)
∵直线y=$\frac{3}{4}$x−3与x轴、y轴分别交于点A,B,
∴点A的坐标为(4,0),点B的坐标为(0,−3),
∴OA=4,OB=3,
∴AB=$\sqrt{3²+4²}$=5.
(2)
∵直线AB的函数解析式为y=$\frac{3}{4}$x−3,
∴过点P(0,4)且垂直于AB的直线的函数解析式为y=−$\frac{4}{3}$x+4.
由$\begin{cases}y=\frac{3}{4}x - 3\\y=-\frac{4}{3}x + 4\end{cases}$解得$\begin{cases}x=\frac{84}{25}\\y=-\frac{12}{25}\end{cases}$.
根据垂线段最短可知点M的坐标为($\frac{84}{25}$,$-\frac{12}{25}$)时,PM最短,此时$PM=\sqrt{(\frac{84}{25})^{2}+(4+\frac{12}{25})^{2}}=\frac{28}{5}$.
(3)如答图,过点C作CM⊥AB于点M,连接AC.

由三角形面积公式得,$\frac{1}{2}$×AB×CM=$\frac{1}{2}$×OA×BC,
∴5×CM=16,
∴CM=$\frac{16}{5}$,
∴圆C上的点到直线y=$\frac{3}{4}$x−3的最大距离是1+$\frac{16}{5}$=$\frac{21}{5}$,
圆C上的点到直线y=$\frac{3}{4}$x−3的最小距离是$\frac{16}{5}$−1 =$\frac{11}{5}$,
∴△PAB面积的最大值是$\frac{1}{2}$×5×$\frac{21}{5}$=$\frac{21}{2}$,
△PAB面积的最小值是$\frac{1}{2}$×5×$\frac{11}{5}$=$\frac{11}{2}$,
∴△PAB面积的最小值与最大值之和是$\frac{21}{2}$+$\frac{11}{2}$=16.
解:
(1)
∵直线y=$\frac{3}{4}$x−3与x轴、y轴分别交于点A,B,
∴点A的坐标为(4,0),点B的坐标为(0,−3),
∴OA=4,OB=3,
∴AB=$\sqrt{3²+4²}$=5.
(2)
∵直线AB的函数解析式为y=$\frac{3}{4}$x−3,
∴过点P(0,4)且垂直于AB的直线的函数解析式为y=−$\frac{4}{3}$x+4.
由$\begin{cases}y=\frac{3}{4}x - 3\\y=-\frac{4}{3}x + 4\end{cases}$解得$\begin{cases}x=\frac{84}{25}\\y=-\frac{12}{25}\end{cases}$.
根据垂线段最短可知点M的坐标为($\frac{84}{25}$,$-\frac{12}{25}$)时,PM最短,此时$PM=\sqrt{(\frac{84}{25})^{2}+(4+\frac{12}{25})^{2}}=\frac{28}{5}$.
(3)如答图,过点C作CM⊥AB于点M,连接AC.

由三角形面积公式得,$\frac{1}{2}$×AB×CM=$\frac{1}{2}$×OA×BC,
∴5×CM=16,
∴CM=$\frac{16}{5}$,
∴圆C上的点到直线y=$\frac{3}{4}$x−3的最大距离是1+$\frac{16}{5}$=$\frac{21}{5}$,
圆C上的点到直线y=$\frac{3}{4}$x−3的最小距离是$\frac{16}{5}$−1 =$\frac{11}{5}$,
∴△PAB面积的最大值是$\frac{1}{2}$×5×$\frac{21}{5}$=$\frac{21}{2}$,
△PAB面积的最小值是$\frac{1}{2}$×5×$\frac{11}{5}$=$\frac{11}{2}$,
∴△PAB面积的最小值与最大值之和是$\frac{21}{2}$+$\frac{11}{2}$=16.
查看更多完整答案,请扫码查看


