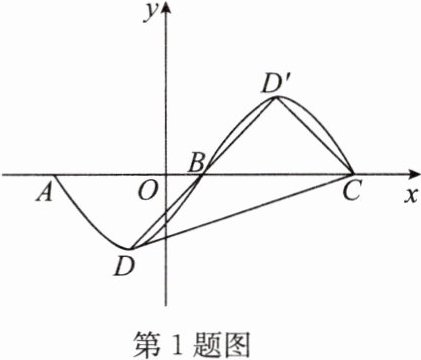
1. 如图,抛物线 $ y = ax^{2}+2ax - 3a(a>0) $ 与 $ x $ 轴交于 $ A,B $ 两点,顶点为 $ D $,把抛物线在 $ x $ 轴下方部分关于点 $ B $ 作中心对称,点 $ D $ 的对应点为 $ D' $,点 $ A $ 的对应点为 $ C $,连接 $ DD',CD',DC $。当 $ \triangle CDD' $ 是直角三角形时,$ a $ 的值为 (
A.$ \frac{1}{2} $ 或 $ \frac{\sqrt{3}}{2} $
B.$ \frac{1}{3} $ 或 $ \frac{\sqrt{3}}{2} $
C.$ \frac{1}{3} $ 或 $ \frac{\sqrt{3}}{3} $
D.$ \frac{1}{2} $ 或 $ \frac{\sqrt{3}}{3} $
A
)
A.$ \frac{1}{2} $ 或 $ \frac{\sqrt{3}}{2} $
B.$ \frac{1}{3} $ 或 $ \frac{\sqrt{3}}{2} $
C.$ \frac{1}{3} $ 或 $ \frac{\sqrt{3}}{3} $
D.$ \frac{1}{2} $ 或 $ \frac{\sqrt{3}}{3} $
答案:
A 点拨:
∵y=ax²+2ax−3a=a(x+3)(x−1)=a(x+1)²−4a,
∴A(−3,0),B(1,0),D(−1,−4a),
∴D’(3,4a),C(5,0).
∵△CDD'是直角三角形,
∴当∠DD'C=90°时,4a=$\frac{1}{2}$×(5−1)=2,得a=$\frac{1}{2}$;当∠D'CD=90°时,CB=$\frac{1}{2}$DD',
∴5−1=$\frac{1}{2}$√[3−(−1)]²+[4a−(−4a)]²,
解得a₁=$\frac{\sqrt{3}}{2}$,a₂=−$\frac{\sqrt{3}}{2}$(舍去).
综上可得,a的值是$\frac{1}{2}$或$\frac{\sqrt{3}}{2}$.
∵y=ax²+2ax−3a=a(x+3)(x−1)=a(x+1)²−4a,
∴A(−3,0),B(1,0),D(−1,−4a),
∴D’(3,4a),C(5,0).
∵△CDD'是直角三角形,
∴当∠DD'C=90°时,4a=$\frac{1}{2}$×(5−1)=2,得a=$\frac{1}{2}$;当∠D'CD=90°时,CB=$\frac{1}{2}$DD',
∴5−1=$\frac{1}{2}$√[3−(−1)]²+[4a−(−4a)]²,
解得a₁=$\frac{\sqrt{3}}{2}$,a₂=−$\frac{\sqrt{3}}{2}$(舍去).
综上可得,a的值是$\frac{1}{2}$或$\frac{\sqrt{3}}{2}$.
2. 某数学兴趣小组根据学习函数的经验,对分段函数 $ y= \begin{cases}ax^{2}+bx - 3(x\geqslant1)\\x^{2}-1(x<1)\end{cases} $ 的图象与性质进行了探究,请补充完整以下探究过程。
| $ x $ | …$ $ | $ -2 $ | $ -1 $ | $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | …$ $ |
| $ y $ | …$ $ | $ 3 $ | $ 0 $ | $ -1 $ | $ 0 $ | $ 1 $ | $ 0 $ | $ -3 $ | …$ $ |
(1) 填空:$ a = $______,$ b = $______。
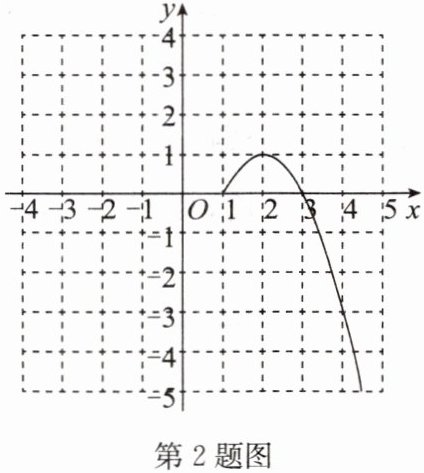
(2) ① 根据上述表格补全如图所示的函数图象;
② 该函数图象是关于______对称的______(填“轴对称”或“中心对称”)图形。
(3) 若直线 $ y= \frac{1}{2}x + t $ 与该函数图象有三个交点,则 $ t $ 的取值范围为______。
| $ x $ | …$ $ | $ -2 $ | $ -1 $ | $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | …$ $ |
| $ y $ | …$ $ | $ 3 $ | $ 0 $ | $ -1 $ | $ 0 $ | $ 1 $ | $ 0 $ | $ -3 $ | …$ $ |
(1) 填空:$ a = $______,$ b = $______。
(2) ① 根据上述表格补全如图所示的函数图象;
② 该函数图象是关于______对称的______(填“轴对称”或“中心对称”)图形。
(3) 若直线 $ y= \frac{1}{2}x + t $ 与该函数图象有三个交点,则 $ t $ 的取值范围为______。

答案:
(1)−1 4 点拨:把(1,0),(2,1)代入y=ax²+bx−3,得$\begin{cases}a + b - 3 = 0\\4a + 2b - 3 = 1\end{cases}$,解得$\begin{cases}a = -1\\b = 4\end{cases}$.
(2)①解:函数图象如答图所示.

②点(1,0) 中心对称
(3)−$\frac{17}{16}$<t<$\frac{1}{16}$ 点拨:联立方程组$\begin{cases}y = \frac{1}{2}x + t\\y = x² - 1\end{cases}$,
消去y,得2x²−x−2−2t=0,
当Δ=0时,即1 + 16 + 16t = 0,解得t = −$\frac{17}{16}$.
联立方程组$\begin{cases}y = \frac{1}{2}x + t\\y = -x² + 4x - 3\end{cases}$,
消去y,得2x²−7x + 2t + 6 = 0,
当Δ=0时,即49 - 16t - 48 = 0,解得t = $\frac{1}{16}$.
观察图象可知,当−$\frac{17}{16}$<t<$\frac{1}{16}$时,直线y = $\frac{1}{2}$x + t与该函数图象有三个交点,
∴t的取值范围为−$\frac{17}{16}$<t<$\frac{1}{16}$.
(1)−1 4 点拨:把(1,0),(2,1)代入y=ax²+bx−3,得$\begin{cases}a + b - 3 = 0\\4a + 2b - 3 = 1\end{cases}$,解得$\begin{cases}a = -1\\b = 4\end{cases}$.
(2)①解:函数图象如答图所示.

②点(1,0) 中心对称
(3)−$\frac{17}{16}$<t<$\frac{1}{16}$ 点拨:联立方程组$\begin{cases}y = \frac{1}{2}x + t\\y = x² - 1\end{cases}$,
消去y,得2x²−x−2−2t=0,
当Δ=0时,即1 + 16 + 16t = 0,解得t = −$\frac{17}{16}$.
联立方程组$\begin{cases}y = \frac{1}{2}x + t\\y = -x² + 4x - 3\end{cases}$,
消去y,得2x²−7x + 2t + 6 = 0,
当Δ=0时,即49 - 16t - 48 = 0,解得t = $\frac{1}{16}$.
观察图象可知,当−$\frac{17}{16}$<t<$\frac{1}{16}$时,直线y = $\frac{1}{2}$x + t与该函数图象有三个交点,
∴t的取值范围为−$\frac{17}{16}$<t<$\frac{1}{16}$.
查看更多完整答案,请扫码查看


