《2025年启东中学作业本九年级数学上册人教版》

3. 定义：将函数 $ C_{1} $ 的图象绕点 $ P(m,0) $ 旋转 $ 180^{\circ} $,得到新的函数 $ C_{2} $ 的图象,我们称函数 $ C_{2} $ 是函数 $ C_{1} $ 关于点 $ P $ 的相关函数。
(1) 当 $ m = 0 $ 时,
① 一次函数 $ y = -x + 7 $ 关于点 $ P $ 的相关函数为y=−x−7；
② 二次函数 $ y = ax^{2}-2ax + a(a\neq0) $ 关于点 $ P $ 的相关函数为y=−a(x+1)²。
(2) 如果函数 $ y= (x - 2)^{2}+6 $ 关于点 $ P $ 的相关函数是 $ y = -(x - 10)^{2}-6 $,那么 $ m = $6。
(3) 若 $ m\geqslant\frac{1}{2} $,当 $ m - 1\leqslant x\leqslant m + 2 $ 时,函数 $ y = x^{2}-6mx + 4m^{2} $ 关于点 $ P(m,0) $ 的相关函数的最大值为 $ 8 $,求 $ m $ 的值。
解:y=x²−6mx+4m²=(x−3m)²−5m²,
∴y=x²−6mx+4m²关于点P(m,0)的相关函数为y=−(x+m)²+5m².
∵m≥$\frac{1}{2}$,∴−m≤m−1,
∴当x=m−1时,y取得最大值8,
∴−(m−1+m)²+5m²=8,整理,得m²+4m−9=0,解得m₁=−2−√13(舍去),m₂=−2+√13,
∴m的值为−2+√13.

答案：
(1)①y=−x−7　②y=−a(x+1)²
(2)6　点拨:函数y=(x−2)²+6图象的顶点坐标为(2,6),函数y=−(x−10)²−6图象的顶点坐标为(10,−6).
∵两个二次函数图象的顶点关于点P(m,0)成中心对称,
∴m=$\frac{2 + 10}{2}$ = 6.
(3)解:y=x²−6mx+4m²=(x−3m)²−5m²,
∴y=x²−6mx+4m²关于点P(m,0)的相关函数为y=−(x+m)²+5m².
∵m≥$\frac{1}{2}$,
∴−m≤m−1,
∴当x=m−1时,y取得最大值8,
∴−(m−1+m)²+5m²=8,整理,得m²+4m−9=0,解得m₁=−2−√13(舍去),m₂=−2+√13,
∴m的值为−2+√13.

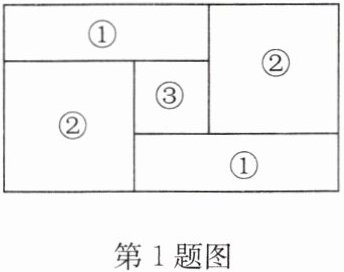
1. 如图,小明家的住房平面图呈矩形,被分割成3个正方形和2个矩形后仍是中心对称图形。若只知道原住房平面图矩形的周长,则分割后不用测量就能知道周长的图形的标号为______。

答案：
①②　点拨:如答图，设图形①的长和宽分别是a,c,图形②的边长是b,图形③的边长是d,原来大长方形的周长是l,则l=2(a+2b+c)。
根据答图可得{a = b + d, ①
{b = c + d, ②
① - ②,得a - b = b - c,
∴2b = a + c。
∴l = 2(a + 2b + c)=2×2(a + c)=4(a + c),或l = 2(a + 2b + c)=2×4b = 8b,
∴2(a + c)=$\frac{l}{2}$,4b = $\frac{l}{2}$。
∴图形①的周长是2(a + c)=$\frac{l}{2}$,图形②的周长是4b = $\frac{l}{2}$,又l为定值。
∴图形①②的周长是定值，不用测量就能知道，图形③的周长不用测量无法知道。
∴分割后不用测量就能知道周长的图形的标号为①②。