《2025年同步跟踪全程检测六年级数学上册苏教版》

3. 怀山药被医家评价为“温补”“性平”,是药食同源的典范。用它来做怀山米粉,需要准备怀山粉与米粉,且怀山粉与米粉的质量比是$2:5$,那么一罐420克的怀山米粉含怀山粉(120)克。

答案： 120 ［解析：由题意可知，怀山粉的质量占怀山米粉的$\frac{2}{2+5}$，因此一罐 420 克的怀山米粉含怀山粉$420×\frac{2}{2+5}=120$(克)。］

4. 在○里填“＞”“＜”或“=”。
$73×\frac {9}{10}$＜73 $\frac {7}{5}÷\frac {3}{8}$＞$\frac {3}{8}$ $7×\frac {7}{8}$=$7÷\frac {8}{7}$

答案： ＜ ＞ =

5. 亮点原创·近年来,中国新能源汽车在全球市场持续保持领先地位,引领着全球汽车产业的转型浪潮。一种新能源汽车行驶10千米约耗电$\frac {3}{2}$千瓦时,这种汽车耗电1千瓦时大约能行驶($\frac{20}{3}$)千米;妈妈开这种新能源汽车去相距45千米远的外婆家,约耗电($\frac{27}{4}$)千瓦时。

答案： $\frac{20}{3}$ $\frac{27}{4}$

6. 用棱长是1厘米的小正方体搭成一个模型,从正面看是,从上面看是,从右面看是,这个模型的体积是(6)立方厘米,表面积是(22)平方厘米。

答案： 6 22

7. 一块长方体木材,长16厘米,宽15厘米,高5厘米,若锯成最大的正方体木块(要求不能割补),则这块正方体木块的体积是(125)立方厘米,最多可以锯成(9)块。

答案： 125 9

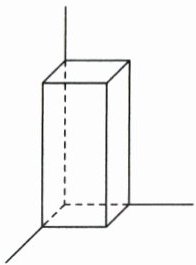
8. 一个长、宽都为4分米的长方体木箱(如右图) 靠在墙角,它露在外面的面积是112平方分米,这个木箱的体积是(192)立方分米。

答案： 192

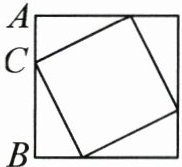
9. 如图,已知大正方形的周长是60分米,它是由4个完全相同的直角三角形和一个小正方形组成的,$AC:CB= 1:2$,其中一个直角三角形的面积是(25)平方分米,小正方形的面积是(125)平方分米。

答案： 25 125 ［解析：根据大正方形的周长是 60 分米，求出大正方形的边长为$60÷4=15$(分米)，由$AC:CB=1:2$，可得$AC=15×\frac{1}{1+2}=5$(分米)，$CB=15×\frac{2}{1+2}=10$(分米)，因此一个直角三角形的面积为$10×5÷2=25$(平方分米)；小正方形的面积=大正方形的面积-四个直角三角形的面积，即$15×15-25×4=125$(平方分米)。］

10. 甲、乙、丙三个仓库共存粮85吨,甲仓库比乙仓库多存粮1吨,丙仓库与乙仓库存粮吨数的比是$3:2$。甲仓库存粮(25)吨。

答案： 25 ［解析：假设甲仓库与乙仓库存粮吨数相等，则三个仓库共存粮$85-1=84$(吨)，且此时甲、乙、丙三个仓库存粮吨数的比为$2:2:3$，再用按比分配的方法求出乙仓库存粮的吨数，最后用乙仓库存粮的吨数加上 1 即可求出甲仓库存粮的吨数。］

11. (南通如东县期末)将一个棱长是1分米的正方体每个面都涂上红色,如果切成1000个相同的小正方体,3面涂色的小正方体有(8)个;如果切成125个相同的小正方体,1面涂色的小正方体有(54)个。

答案： 8 54 ［解析：顶点上的小正方体 3 面涂色，所以有 8 个。因为$125=5×5×5$，所以 1 面涂色的小正方体有$(5-2)×(5-2)×6=54$(个)。］

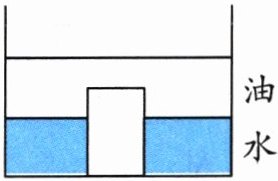
12. 如图,有一个足够深的水槽,底面是长为16厘米、宽为12厘米的长方形,原来在水槽里盛有6厘米深的水和6厘米深的油(油在水上方)。在水槽中放入一个长、宽、高分别为8厘米、6厘米、12厘米的铁块,那么此时油层的高度是(7)厘米。

答案： 7 ［解析：原来水槽中的水的体积是$16×12×6=1152$(立方厘米)，放入铁块后，水的高度变为$1152÷(16×12-8×6)=8$(厘米)，所以仍有$12-8=4$(厘米)高的铁块在油里，则油层增加的高度是$8×6×4÷(16×12)=1$(厘米)，因此此时油层的高度是$1+6=7$(厘米)。］