《2025年快乐假期暑假作业延边教育出版社八年级数学北师大版》

7. 如图所示的四个图形中，图形①与图形④成轴对称，图形①与图形③成中心对称.(填写符合要求的图形所对应的序号)

答案： ④ ③

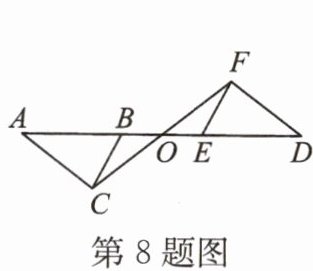
8. 如图，△ABC与△DEF关于点O成中心对称，则AB=DE，BC//EF，AC=DF.

答案： = EF DF

9. 如图是4×4的正方形网格，把其中一个标有数字的白色小正方形涂黑，就可以使图中的黑色部分构成一个中心对称图形，则这个白色小正方形内的数字是3.

答案： 3

10. 象棋中也有很多数学知识，如图，我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1)，根据象棋中“马”走“日”的规定，若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标：(0,0),(0,2),(1,3),(3,3),(4,2),(4,0).
(2)解答下列两个问题：
①如果顺次连接(1)中的所有点，得到的图形是轴对称图形(填“中心对称”“旋转对称”或“轴对称”)；
②(1)中关于点P成中心对称的点的坐标为(0,0)和(4,2),(0,2)和(4,0).

答案：
(1)(0,0),(0,2),(1,3),(3,3),(4,2),(4,0)
(2)①轴对称 ②(0,0)和(4,2),(0,2)和(4,0)

11. 如图，直线l与直线m相交于点P，作出△ABC关于点P成中心对称的图形.

按照上述步骤作出的△A'B'C'

答案： 【解析】：
1. 连接$AP$并延长至$A'$，使$PA' = PA$，则点$A'$是点$A$关于点$P$的对称点。
理由：根据中心对称的性质，对应点的连线经过对称中心，且被对称中心平分。
2. 连接$BP$并延长至$B'$，使$PB' = PB$，则点$B'$是点$B$关于点$P$的对称点。
理由：同理，利用中心对称对应点的性质。
3. 连接$CP$并延长至$C'$，使$PC' = PC$，则点$C'$是点$C$关于点$P$的对称点。
理由：依据中心对称对应点连线与对称中心的关系。
4. 顺次连接$A'$、$B'$、$C'$，$\triangle A'B'C'$就是$\triangle ABC$关于点$P$成中心对称的图形。
理由：由中心对称的定义，三个对应点都关于点$P$对称，所以连接后得到的图形就是所求的中心对称图形。
【答案】：按照上述步骤作出的$\triangle A'B'C'$ 。