第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
例4 有20袋大米,以25 kg标准质量为准,超过或不足的千克数分别用正负数来表示,记录如下:
与标准质量的差值/kg
-1.5
-1
-0.5
0
+0.5
+1
袋数
1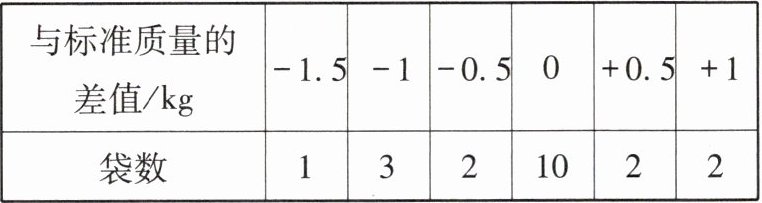
(1)求这20袋大米的平均质量;
(2)每袋大米的标准质量是25 kg,售价为6元/kg,则这些大米可卖多少元?
解:(1)(-1.5×1)+(-1×3)+(-0.5×2)+(0×10)+(0.5×2)+(1×2)
=-1.5-3-2.5+0+2.5+2
=-2.5(kg),
25-2.5÷20= 24.875(kg).
答:20袋大米的平均质量为24.875 kg.
(2)(25×20-2.5)×6
=(500-2.5)×6
=487.5×6
=2985(元).
答:这些大米可卖2985元.
与标准质量的差值/kg
-1.5
-1
-0.5
0
+0.5
+1
袋数
1

(1)求这20袋大米的平均质量;
(2)每袋大米的标准质量是25 kg,售价为6元/kg,则这些大米可卖多少元?
解:(1)(-1.5×1)+(-1×3)+(-0.5×2)+(0×10)+(0.5×2)+(1×2)
=-1.5-3-2.5+0+2.5+2
=-2.5(kg),
25-2.5÷20= 24.875(kg).
答:20袋大米的平均质量为24.875 kg.
(2)(25×20-2.5)×6
=(500-2.5)×6
=487.5×6
=2985(元).
答:这些大米可卖2985元.
答案:
例4 有20袋大米,以25 kg标准质量为准,超过或不足的千克数分别用正负数来表示,记录如下:
与标准质量的差值/kg
-1.5
-1
-0.5
0
+0.5
+1
袋数
1
(1)求这20袋大米的平均质量;
(2)每袋大米的标准质量是25 kg,售价为6元/kg,则这些大米可卖多少元?
解:(1)(-1.5×1)+(-1×3)+(-0.5×2)+(0×10)+(0.5×2)+(1×2)
=-1.5-3-2.5+0+2.5+2
=-2.5(kg),
25-2.5÷20= 24.875(kg).
答:20袋大米的平均质量为24.875 kg.
(2)(25×20-2.5)×6
=(500-2.5)×6
=487.5×6
=2985(元).
答:这些大米可卖2985元.
与标准质量的差值/kg
-1.5
-1
-0.5
0
+0.5
+1
袋数
1

(1)求这20袋大米的平均质量;
(2)每袋大米的标准质量是25 kg,售价为6元/kg,则这些大米可卖多少元?
解:(1)(-1.5×1)+(-1×3)+(-0.5×2)+(0×10)+(0.5×2)+(1×2)
=-1.5-3-2.5+0+2.5+2
=-2.5(kg),
25-2.5÷20= 24.875(kg).
答:20袋大米的平均质量为24.875 kg.
(2)(25×20-2.5)×6
=(500-2.5)×6
=487.5×6
=2985(元).
答:这些大米可卖2985元.
答案:
例4 有20袋大米,以25 kg标准质量为准,超过或不足的千克数分别用正负数来表示,记录如下:
与标准质量的差值/kg
-1.5
-1
-0.5
0
+0.5
+1
袋数
1
(1)求这20袋大米的平均质量;
(2)每袋大米的标准质量是25 kg,售价为6元/kg,则这些大米可卖多少元?
解:(1)(-1.5×1)+(-1×3)+(-0.5×2)+(0×10)+(0.5×2)+(1×2)
=-1.5-3-2.5+0+2.5+2
=-2.5(kg),
25-2.5÷20= 24.875(kg).
答:20袋大米的平均质量为24.875 kg.
(2)(25×20-2.5)×6
=(500-2.5)×6
=487.5×6
=2985(元).
答:这些大米可卖2985元.
与标准质量的差值/kg
-1.5
-1
-0.5
0
+0.5
+1
袋数
1

(1)求这20袋大米的平均质量;
(2)每袋大米的标准质量是25 kg,售价为6元/kg,则这些大米可卖多少元?
解:(1)(-1.5×1)+(-1×3)+(-0.5×2)+(0×10)+(0.5×2)+(1×2)
=-1.5-3-2.5+0+2.5+2
=-2.5(kg),
25-2.5÷20= 24.875(kg).
答:20袋大米的平均质量为24.875 kg.
(2)(25×20-2.5)×6
=(500-2.5)×6
=487.5×6
=2985(元).
答:这些大米可卖2985元.
答案:
1.老师设计了一个计算程序如图所示:
当x= -6时,输出的结果为

当x= -6时,输出的结果为
2
.
答案:
2
1.老师设计了一个计算程序如图所示:
当x= -6时,输出的结果为

当x= -6时,输出的结果为
2
.
答案:
2
1.老师设计了一个计算程序如图所示:
当x= -6时,输出的结果为

当x= -6时,输出的结果为
2
.
答案:
2
2.规定一种新运算:a△b= aᵇ,a▽b= bᵃ,其中a,b为有理数.计算:
(1)0△1=
(2)2▽(-3)=
(1)0△1=
0
;(2)2▽(-3)=
9
.
答案:
0 9
2.规定一种新运算:a△b= aᵇ,a▽b= bᵃ,其中a,b为有理数.计算:
(1)0△1=
(2)2▽(-3)=
(1)0△1=
0
;(2)2▽(-3)=
9
.
答案:
0 9
2.规定一种新运算:a△b= aᵇ,a▽b= bᵃ,其中a,b为有理数.计算:
(1)0△1=
(2)2▽(-3)=
(1)0△1=
0
;(2)2▽(-3)=
9
.
答案:
0 9
3.计算:
(1)-2^3÷$\frac{4}{9}$×(-$\frac{2}{3}$)^2;
(2)(-7)×(-5)-90÷(-15);
(3)-5^2-[-4-(1+$\frac{1}{5}$÷0.2)÷(-2)];
(4)4.27×(-$\frac{6}{11}$)-8.73×$\frac{6}{11}$-2×(-$\frac{6}{11}$).
解:(1)原式= -8×($\frac{9}{4}$×$\frac{4}{9}$)
=-8×1
=-8;
(2)原式= 35-(-6)
=41;
(3)原式= -25-[-4-(1+1)÷(-2)]
=-25-(-4+1)
=-25+3
=-22;
(4)原式= -4.27×$\frac{6}{11}$-8.73×$\frac{6}{11}$+2×$\frac{6}{11}$
=$\frac{6}{11}$×(-4.27-8.73+2)
=$\frac{6}{11}$×(-11)
=-6.
(1)-2^3÷$\frac{4}{9}$×(-$\frac{2}{3}$)^2;
(2)(-7)×(-5)-90÷(-15);
(3)-5^2-[-4-(1+$\frac{1}{5}$÷0.2)÷(-2)];
(4)4.27×(-$\frac{6}{11}$)-8.73×$\frac{6}{11}$-2×(-$\frac{6}{11}$).
解:(1)原式= -8×($\frac{9}{4}$×$\frac{4}{9}$)
=-8×1
=-8;
(2)原式= 35-(-6)
=41;
(3)原式= -25-[-4-(1+1)÷(-2)]
=-25-(-4+1)
=-25+3
=-22;
(4)原式= -4.27×$\frac{6}{11}$-8.73×$\frac{6}{11}$+2×$\frac{6}{11}$
=$\frac{6}{11}$×(-4.27-8.73+2)
=$\frac{6}{11}$×(-11)
=-6.
答案:
3.计算:
(1)-2^3÷$\frac{4}{9}$×(-$\frac{2}{3}$)^2;
(2)(-7)×(-5)-90÷(-15);
(3)-5^2-[-4-(1+$\frac{1}{5}$÷0.2)÷(-2)];
(4)4.27×(-$\frac{6}{11}$)-8.73×$\frac{6}{11}$-2×(-$\frac{6}{11}$).
解:(1)原式= -8×($\frac{9}{4}$×$\frac{4}{9}$)
=-8×1
=-8;
(2)原式= 35-(-6)
=41;
(3)原式= -25-[-4-(1+1)÷(-2)]
=-25-(-4+1)
=-25+3
=-22;
(4)原式= -4.27×$\frac{6}{11}$-8.73×$\frac{6}{11}$+2×$\frac{6}{11}$
=$\frac{6}{11}$×(-4.27-8.73+2)
=$\frac{6}{11}$×(-11)
=-6.
(1)-2^3÷$\frac{4}{9}$×(-$\frac{2}{3}$)^2;
(2)(-7)×(-5)-90÷(-15);
(3)-5^2-[-4-(1+$\frac{1}{5}$÷0.2)÷(-2)];
(4)4.27×(-$\frac{6}{11}$)-8.73×$\frac{6}{11}$-2×(-$\frac{6}{11}$).
解:(1)原式= -8×($\frac{9}{4}$×$\frac{4}{9}$)
=-8×1
=-8;
(2)原式= 35-(-6)
=41;
(3)原式= -25-[-4-(1+1)÷(-2)]
=-25-(-4+1)
=-25+3
=-22;
(4)原式= -4.27×$\frac{6}{11}$-8.73×$\frac{6}{11}$+2×$\frac{6}{11}$
=$\frac{6}{11}$×(-4.27-8.73+2)
=$\frac{6}{11}$×(-11)
=-6.
答案:
3.计算:
(1)-2^3÷$\frac{4}{9}$×(-$\frac{2}{3}$)^2;
(2)(-7)×(-5)-90÷(-15);
(3)-5^2-[-4-(1+$\frac{1}{5}$÷0.2)÷(-2)];
(4)4.27×(-$\frac{6}{11}$)-8.73×$\frac{6}{11}$-2×(-$\frac{6}{11}$).
解:(1)原式= -8×($\frac{9}{4}$×$\frac{4}{9}$)
=-8×1
=-8;
(2)原式= 35-(-6)
=41;
(3)原式= -25-[-4-(1+1)÷(-2)]
=-25-(-4+1)
=-25+3
=-22;
(4)原式= -4.27×$\frac{6}{11}$-8.73×$\frac{6}{11}$+2×$\frac{6}{11}$
=$\frac{6}{11}$×(-4.27-8.73+2)
=$\frac{6}{11}$×(-11)
=-6.
(1)-2^3÷$\frac{4}{9}$×(-$\frac{2}{3}$)^2;
(2)(-7)×(-5)-90÷(-15);
(3)-5^2-[-4-(1+$\frac{1}{5}$÷0.2)÷(-2)];
(4)4.27×(-$\frac{6}{11}$)-8.73×$\frac{6}{11}$-2×(-$\frac{6}{11}$).
解:(1)原式= -8×($\frac{9}{4}$×$\frac{4}{9}$)
=-8×1
=-8;
(2)原式= 35-(-6)
=41;
(3)原式= -25-[-4-(1+1)÷(-2)]
=-25-(-4+1)
=-25+3
=-22;
(4)原式= -4.27×$\frac{6}{11}$-8.73×$\frac{6}{11}$+2×$\frac{6}{11}$
=$\frac{6}{11}$×(-4.27-8.73+2)
=$\frac{6}{11}$×(-11)
=-6.
答案:
对于有理数a,b,定义新运算“△”,规则如下:a△b= ab-a-b+4,如:3△5= 3×5-3-5+4= 11.
(1)求3△(-4)的值.
(2)请你判断交换律在“△”运算中是否成立?并给出证明.
解:(1)∵a△b= ab-a-b+4,
∴3△(-4)
=3×(-4)-3-(-4)+4
=-12+(-3)+4+4
=-7;
(2)交换律在“△”运算中成立,
理由:由题意可得,a△b= ab-a-b+4,b△a= ab-b-a+4,
∴a△b= b△a,
∴交换律在“△”运算中成立.
(1)求3△(-4)的值.
(2)请你判断交换律在“△”运算中是否成立?并给出证明.
解:(1)∵a△b= ab-a-b+4,
∴3△(-4)
=3×(-4)-3-(-4)+4
=-12+(-3)+4+4
=-7;
(2)交换律在“△”运算中成立,
理由:由题意可得,a△b= ab-a-b+4,b△a= ab-b-a+4,
∴a△b= b△a,
∴交换律在“△”运算中成立.
答案:
对于有理数a,b,定义新运算“△”,规则如下:a△b= ab-a-b+4,如:3△5= 3×5-3-5+4= 11.
(1)求3△(-4)的值.
(2)请你判断交换律在“△”运算中是否成立?并给出证明.
解:(1)∵a△b= ab-a-b+4,
∴3△(-4)
=3×(-4)-3-(-4)+4
=-12+(-3)+4+4
=-7;
(2)交换律在“△”运算中成立,
理由:由题意可得,a△b= ab-a-b+4,b△a= ab-b-a+4,
∴a△b= b△a,
∴交换律在“△”运算中成立.
(1)求3△(-4)的值.
(2)请你判断交换律在“△”运算中是否成立?并给出证明.
解:(1)∵a△b= ab-a-b+4,
∴3△(-4)
=3×(-4)-3-(-4)+4
=-12+(-3)+4+4
=-7;
(2)交换律在“△”运算中成立,
理由:由题意可得,a△b= ab-a-b+4,b△a= ab-b-a+4,
∴a△b= b△a,
∴交换律在“△”运算中成立.
答案:
对于有理数a,b,定义新运算“△”,规则如下:a△b= ab-a-b+4,如:3△5= 3×5-3-5+4= 11.
(1)求3△(-4)的值.
(2)请你判断交换律在“△”运算中是否成立?并给出证明.
解:(1)∵a△b= ab-a-b+4,
∴3△(-4)
=3×(-4)-3-(-4)+4
=-12+(-3)+4+4
=-7;
(2)交换律在“△”运算中成立,
理由:由题意可得,a△b= ab-a-b+4,b△a= ab-b-a+4,
∴a△b= b△a,
∴交换律在“△”运算中成立.
(1)求3△(-4)的值.
(2)请你判断交换律在“△”运算中是否成立?并给出证明.
解:(1)∵a△b= ab-a-b+4,
∴3△(-4)
=3×(-4)-3-(-4)+4
=-12+(-3)+4+4
=-7;
(2)交换律在“△”运算中成立,
理由:由题意可得,a△b= ab-a-b+4,b△a= ab-b-a+4,
∴a△b= b△a,
∴交换律在“△”运算中成立.
答案:
查看更多完整答案,请扫码查看


