第105页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
【模型构建】若线段上有m个点(包括端点),则该线段上共有____条线段.【拓展应用】若有8位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛. 解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
 解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
答案:
【模型构建】若线段上有m个点(包括端点),则该线段上共有____条线段.【拓展应用】若有8位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛. 解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
 解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
答案:
【模型构建】若线段上有m个点(包括端点),则该线段上共有____条线段.【拓展应用】若有8位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛. 解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
 解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
解:【观察思考】∵以点A为左端点向右的线段有:线段AB,AC,AD,以点C为左端点向右的线段有线段CD,CB,以点D为左端点的线段有线段DB,∴共有3+2+1= 6(条).【模型构建】设线段上有m个点,该线段上共有线段x条,则x= (m-1)+(m-2)+(m-3)+…+3+2+1,∴倒序排列有x= 1+2+3+…+(m-3)+(m-2)+(m-1),∴2x= m+m+m+…+m= m(m-1),∴x= $\frac{1}{2}$m(m-1).故答案为:$\frac{1}{2}$m(m-1);【拓展应用】把8位同学看作直线上的8个点,每两位同学之间的一场比赛看作一条线段,由题知,当m= 8时,$\frac{m(m-1)}{2}$= $\frac{8×(8-1)}{2}$= 28.答:一共要进行28场比赛.
答案:
(  A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
D
) A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
答案:
D
(  A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
D
) A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
答案:
D
(  A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
D
) A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
A. 点C在直线AB上B. 点C在线段AB上C. 点B在射线AC上D. 点B在线段AC上
答案:
D
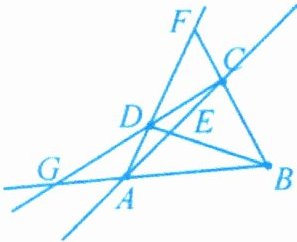
(1)画线段AB,射线AD,直线AC;(2)连接BD,线段BD与直线AC交于点E;(3)连接BC,并延长线段BC与射线AD交于点F;(4)连接CD,并延长线段CD与线段AB的反向延长线交于点G. 解:如图所示.
解:如图所示.
 解:如图所示.
解:如图所示.
答案:
(1)画线段AB,射线AD,直线AC;(2)连接BD,线段BD与直线AC交于点E;(3)连接BC,并延长线段BC与射线AD交于点F;(4)连接CD,并延长线段CD与线段AB的反向延长线交于点G. 解:如图所示.
解:如图所示.

 解:如图所示.
解:如图所示.
答案:
(1)画线段AB,射线AD,直线AC;(2)连接BD,线段BD与直线AC交于点E;(3)连接BC,并延长线段BC与射线AD交于点F;(4)连接CD,并延长线段CD与线段AB的反向延长线交于点G. 解:如图所示.
解:如图所示.

 解:如图所示.
解:如图所示.
答案:
查看更多完整答案,请扫码查看


