《2025年育才课堂探究册七年级数学上册北师大版》

已知线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,D为AC的中点,求BD的长.
解:如图1,∵线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,∴BC= AC+AB= AC+30,
∴$\frac{AC}{AC+30}= \frac{1}{4}$,∴AC= 10,∵D为AC的中点,∴DA= $\frac{1}{2}$AC= $\frac{1}{2}$×10= 5,
∴BD= AB+DA= 30+5= 35;

如图2,∵线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,∴BC= AB-AC,∴$\frac{AC}{AB-AC}= \frac{1}{4}$,
∴$\frac{AC}{30-AC}= \frac{1}{4}$,∴AC= 6,∵D为AC的中点,∴AD= $\frac{1}{2}$AC= $\frac{1}{2}$×6= 3,∴BD= AB-AD= 30-3= 27,综上所述,BD的长为35或27.

答案：

已知线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,D为AC的中点,求BD的长.
解:如图1,∵线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,∴BC= AC+AB= AC+30,
∴$\frac{AC}{AC+30}= \frac{1}{4}$,∴AC= 10,∵D为AC的中点,∴DA= $\frac{1}{2}$AC= $\frac{1}{2}$×10= 5,
∴BD= AB+DA= 30+5= 35;

如图2,∵线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,∴BC= AB-AC,∴$\frac{AC}{AB-AC}= \frac{1}{4}$,
∴$\frac{AC}{30-AC}= \frac{1}{4}$,∴AC= 6,∵D为AC的中点,∴AD= $\frac{1}{2}$AC= $\frac{1}{2}$×6= 3,∴BD= AB-AD= 30-3= 27,综上所述,BD的长为35或27.

答案：

已知线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,D为AC的中点,求BD的长.
解:如图1,∵线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,∴BC= AC+AB= AC+30,
∴$\frac{AC}{AC+30}= \frac{1}{4}$,∴AC= 10,∵D为AC的中点,∴DA= $\frac{1}{2}$AC= $\frac{1}{2}$×10= 5,
∴BD= AB+DA= 30+5= 35;

如图2,∵线段AB= 30,直线AB上有一点C,且AC:BC= 1:4,∴BC= AB-AC,∴$\frac{AC}{AB-AC}= \frac{1}{4}$,
∴$\frac{AC}{30-AC}= \frac{1}{4}$,∴AC= 6,∵D为AC的中点,∴AD= $\frac{1}{2}$AC= $\frac{1}{2}$×6= 3,∴BD= AB-AD= 30-3= 27,综上所述,BD的长为35或27.

答案：

已知∠AOB= 60°,∠BOC= 20°,在其顶点O处引一条射线OD,使OD平分∠AOC,求∠AOD的度数.
解:①当OC在∠AOB外时,如图1所示:

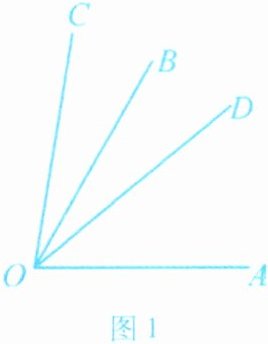
∵∠AOB= 60°,∠BOC= 20°,∴∠AOC= ∠AOB+∠BOC= 80°,∵OD平分∠AOC,
∴∠AOD= $\frac{1}{2}$∠AOC= 40°;
②当OC在∠AOB内时,如图2所示:

∵∠AOB= 60°,∠BOC= 20°,∴∠AOC= ∠AOB-∠BOC= 40°,∵OD平分∠AOC,
∴∠AOD= $\frac{1}{2}$∠AOC= 20°.综上所述:∠AOD的度数为40°或20°.

答案：

已知∠AOB= 60°,∠BOC= 20°,在其顶点O处引一条射线OD,使OD平分∠AOC,求∠AOD的度数.
解:①当OC在∠AOB外时,如图1所示:

∵∠AOB= 60°,∠BOC= 20°,∴∠AOC= ∠AOB+∠BOC= 80°,∵OD平分∠AOC,
∴∠AOD= $\frac{1}{2}$∠AOC= 40°;
②当OC在∠AOB内时,如图2所示:

∵∠AOB= 60°,∠BOC= 20°,∴∠AOC= ∠AOB-∠BOC= 40°,∵OD平分∠AOC,
∴∠AOD= $\frac{1}{2}$∠AOC= 20°.综上所述:∠AOD的度数为40°或20°.

答案：

已知∠AOB= 60°,∠BOC= 20°,在其顶点O处引一条射线OD,使OD平分∠AOC,求∠AOD的度数.
解:①当OC在∠AOB外时,如图1所示:

∵∠AOB= 60°,∠BOC= 20°,∴∠AOC= ∠AOB+∠BOC= 80°,∵OD平分∠AOC,
∴∠AOD= $\frac{1}{2}$∠AOC= 40°;
②当OC在∠AOB内时,如图2所示:

∵∠AOB= 60°,∠BOC= 20°,∴∠AOC= ∠AOB-∠BOC= 40°,∵OD平分∠AOC,
∴∠AOD= $\frac{1}{2}$∠AOC= 20°.综上所述:∠AOD的度数为40°或20°.

答案：

问题情境:七年级数学活动周以探究“线段与角的共性”为主题,同学们通过类比线段的中点与角平分线知识与方法,促进同学们知识迁移与融合能力.
【特例感知】
(1)如图1,已知线段CD在线段AB上运动,线段AB= 10 cm,CD= 2 cm,E,F分别是AC,BD的中点.解答下列问题:
①若AC= 3 cm,则EF的长为_____cm.(直接写出结果)
②小聪发现:保持线段CD在线段AB上运动,其他条件不变,则EF的长保持不变.小聪理由如下:
∵E,F分别是AC,BD的中点,∴EC= $\frac{1}{2}$AC,DF= $\frac{1}{2}$DB,
∴EF= EC+CD+DF= $\frac{1}{2}$AC+CD+$\frac{1}{2}$BD= $\frac{1}{2}$(AC+DB)+CD= $\frac{1}{2}$(AB-CD)+CD= $\frac{1}{2}$(AB+CD),
∵AB= 10 cm,CD= 2 cm不变,∴EF的长不变.
【类比探究】
(2)小聪继续探究发现角与线段类似,如图2,已知∠COD在∠AOB内部转动,OE和OF分别平分∠AOC和∠BOD,则∠EOF与∠AOB,∠COD有数量关系,说明理由.
【知识迁移】
(3)如图3,已知∠COD在∠AOB内部转动,若∠AOB= 150°,∠COD= 30°,∠AOE= k∠EOC,∠BOF= k∠DOF,求∠EOF= _____.(用含有k的式子表示)

解:(2)∠EOF= $\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD,理由如下:
∵OE和OF分别平分∠AOC和∠BOD,∴∠AOE= ∠COE= $\frac{1}{2}$∠AOC,∠BOF= ∠DOF= $\frac{1}{2}$∠BOD,
∴∠EOF= ∠EOC+∠COD+∠DOF= $\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOD+∠COD= $\frac{1}{2}$(∠AOC+∠BOD)+∠COD
=$\frac{1}{2}$(∠AOB-∠COD)+∠COD= $\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD;
(3)∵∠AOE= k∠EOC,∠BOF= k∠DOF,∴∠EOC= $\frac{1}{1+k}$∠AOC,∠DOF= $\frac{1}{1+k}$∠BOD,
∴∠EOF= $\frac{1}{1+k}$∠AOC+$\frac{1}{1+k}$∠BOD+∠COD= $\frac{1}{1+k}$·(∠AOC+∠BOD)+∠COD= $\frac{1}{1+k}$×120°+30°= $\frac{120^\circ}{1+k}$+30°.故答案为:$\frac{120^\circ}{1+k}$+30°.

答案： 6 $\frac{120^\circ}{1+k}+30^\circ$

问题情境:七年级数学活动周以探究“线段与角的共性”为主题,同学们通过类比线段的中点与角平分线知识与方法,促进同学们知识迁移与融合能力.
【特例感知】
(1)如图1,已知线段CD在线段AB上运动,线段AB= 10 cm,CD= 2 cm,E,F分别是AC,BD的中点.解答下列问题:
①若AC= 3 cm,则EF的长为_____cm.(直接写出结果)
②小聪发现:保持线段CD在线段AB上运动,其他条件不变,则EF的长保持不变.小聪理由如下:
∵E,F分别是AC,BD的中点,∴EC= $\frac{1}{2}$AC,DF= $\frac{1}{2}$DB,
∴EF= EC+CD+DF= $\frac{1}{2}$AC+CD+$\frac{1}{2}$BD= $\frac{1}{2}$(AC+DB)+CD= $\frac{1}{2}$(AB-CD)+CD= $\frac{1}{2}$(AB+CD),
∵AB= 10 cm,CD= 2 cm不变,∴EF的长不变.
【类比探究】
(2)小聪继续探究发现角与线段类似,如图2,已知∠COD在∠AOB内部转动,OE和OF分别平分∠AOC和∠BOD,则∠EOF与∠AOB,∠COD有数量关系,说明理由.
【知识迁移】
(3)如图3,已知∠COD在∠AOB内部转动,若∠AOB= 150°,∠COD= 30°,∠AOE= k∠EOC,∠BOF= k∠DOF,求∠EOF= _____.(用含有k的式子表示)

解:(2)∠EOF= $\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD,理由如下:
∵OE和OF分别平分∠AOC和∠BOD,∴∠AOE= ∠COE= $\frac{1}{2}$∠AOC,∠BOF= ∠DOF= $\frac{1}{2}$∠BOD,
∴∠EOF= ∠EOC+∠COD+∠DOF= $\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOD+∠COD= $\frac{1}{2}$(∠AOC+∠BOD)+∠COD
=$\frac{1}{2}$(∠AOB-∠COD)+∠COD= $\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD;
(3)∵∠AOE= k∠EOC,∠BOF= k∠DOF,∴∠EOC= $\frac{1}{1+k}$∠AOC,∠DOF= $\frac{1}{1+k}$∠BOD,
∴∠EOF= $\frac{1}{1+k}$∠AOC+$\frac{1}{1+k}$∠BOD+∠COD= $\frac{1}{1+k}$·(∠AOC+∠BOD)+∠COD= $\frac{1}{1+k}$×120°+30°= $\frac{120^\circ}{1+k}$+30°.故答案为:$\frac{120^\circ}{1+k}$+30°.

答案： 6 $\frac{120^\circ}{1+k}+30^\circ$

问题情境:七年级数学活动周以探究“线段与角的共性”为主题,同学们通过类比线段的中点与角平分线知识与方法,促进同学们知识迁移与融合能力.
【特例感知】
(1)如图1,已知线段CD在线段AB上运动,线段AB= 10 cm,CD= 2 cm,E,F分别是AC,BD的中点.解答下列问题:
①若AC= 3 cm,则EF的长为_____cm.(直接写出结果)
②小聪发现:保持线段CD在线段AB上运动,其他条件不变,则EF的长保持不变.小聪理由如下:
∵E,F分别是AC,BD的中点,∴EC= $\frac{1}{2}$AC,DF= $\frac{1}{2}$DB,
∴EF= EC+CD+DF= $\frac{1}{2}$AC+CD+$\frac{1}{2}$BD= $\frac{1}{2}$(AC+DB)+CD= $\frac{1}{2}$(AB-CD)+CD= $\frac{1}{2}$(AB+CD),
∵AB= 10 cm,CD= 2 cm不变,∴EF的长不变.
【类比探究】
(2)小聪继续探究发现角与线段类似,如图2,已知∠COD在∠AOB内部转动,OE和OF分别平分∠AOC和∠BOD,则∠EOF与∠AOB,∠COD有数量关系,说明理由.
【知识迁移】
(3)如图3,已知∠COD在∠AOB内部转动,若∠AOB= 150°,∠COD= 30°,∠AOE= k∠EOC,∠BOF= k∠DOF,求∠EOF= _____.(用含有k的式子表示)

解:(2)∠EOF= $\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD,理由如下:
∵OE和OF分别平分∠AOC和∠BOD,∴∠AOE= ∠COE= $\frac{1}{2}$∠AOC,∠BOF= ∠DOF= $\frac{1}{2}$∠BOD,
∴∠EOF= ∠EOC+∠COD+∠DOF= $\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOD+∠COD= $\frac{1}{2}$(∠AOC+∠BOD)+∠COD
=$\frac{1}{2}$(∠AOB-∠COD)+∠COD= $\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD;
(3)∵∠AOE= k∠EOC,∠BOF= k∠DOF,∴∠EOC= $\frac{1}{1+k}$∠AOC,∠DOF= $\frac{1}{1+k}$∠BOD,
∴∠EOF= $\frac{1}{1+k}$∠AOC+$\frac{1}{1+k}$∠BOD+∠COD= $\frac{1}{1+k}$·(∠AOC+∠BOD)+∠COD= $\frac{1}{1+k}$×120°+30°= $\frac{120^\circ}{1+k}$+30°.故答案为:$\frac{120^\circ}{1+k}$+30°.

答案： 6 $\frac{120^\circ}{1+k}+30^\circ$