《2025年暑假生活指导八年级山东教育出版社》

例1 如图,是某城市街道示意图,$AF// BC$,$EC\perp BC$,$BA// DE$,$BD// AE$。甲、乙两人同时从$B站乘车到F$站,甲乘1路车,路线是$B\rightarrow A\rightarrow E\rightarrow F$；乙乘2路车,路线是$B\rightarrow D\rightarrow C\rightarrow F$。假设两车速度相同,途中耽误的时间相同,那么谁先到达$F$站？请说明理由。

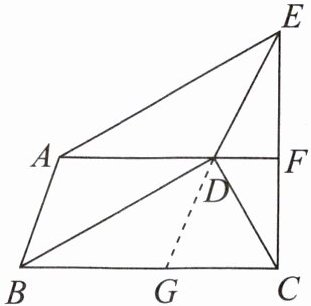
答案： 【解析】：
连接$BE$、$AD$。
因为$BA// DE$，$BD// AE$，所以四边形$ABDE$是平行四边形。
所以$BA + AE = DE + AE = BD + DC = AD + DC$。
因为$AF// BC$，$BA// DE$，所以四边形$ABGD$是平行四边形。
因为$EC\perp BC$，所以$\angle ECD = 90^{\circ}$。
因为$AF// BC$，所以$\angle FDC = \angle DCG = 90^{\circ}$。
因为$BD// AE$，$AF// BC$，所以$\angle EAD = \angle ADG$，$\angle ADG = \angle DAC$（两直线平行，内错角相等），所以$\angle EAD = \angle DAC$。
在$\triangle ADE$和$\triangle ADC$中，
$\begin{cases}AE = DC,\\\angle EAD = \angle DAC,\\AD = AD.\end{cases}$
所以$\triangle ADE\cong\triangle ADC(SAS)$，所以$DE = DC$，$\angle ADE = \angle ADC$。
因为$\angle EDC = \angle EDA + \angle ADC = \angle EDA + \angle ADE = 180^{\circ}$，所以$E$、$D$、$C$三点共线。
因为$AF// BC$，$EC\perp BC$，所以$\angle EFG = \angle ECF = 90^{\circ}$。
因为$BA// DE$，所以$\angle FED = \angle BAE$（两直线平行，同位角相等），所以$\angle FED = \angle BAE = \angle BGD = \angle EGF$，又因为$\angle EFG = \angle ECF = 90^{\circ}$，$EF = EF$，所以$\triangle EFG\cong\triangle ECF(AAS)$，所以$FG = CF$。
所以$EF + CF = EF + FG = EG$，$BA + AE + EF = BD + DC + CF = AD + DC + EG$。
在$\triangle ADG$和$\triangle EDG$中，
$\begin{cases}DG = DG,\\\angle ADG = \angle EDG,\\AD = ED.\end{cases}$
所以$\triangle ADG\cong\triangle EDG(SAS)$，所以$AG = EG$。
所以$BA + AE + EF = BD + DC + CF$，即两条路线长短相同，故两人同时到达。
【答案】：两人同时到达，因为两条路线长短相同。

例2 如图,某村有一个四边形池塘,在它四个角$A$、$B$、$C$、$D$处均有一棵桃树,该村准备扩池塘建养鱼池,既想使池塘的面积扩大到原来的2倍,又想保留原来的四棵桃树不动。为使挖过的池塘更美观,想挖成一个平行四边形,能否实现？若能,请设计出来；若不能,请说明理由。

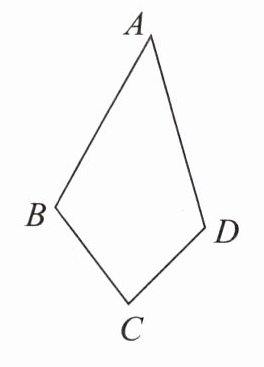
答案：
解析：由于四棵桃树分别在四边形的顶点上,所以要想把池塘挖成一个平行四边形,并且使池塘的面积扩大到原来的2倍,那么,这四棵桃树应在平行四边形的边上,且每个边上都应该有一棵桃树。所以,我们可以经过四个顶点分别作对角线的平行线,如图所示,就能够解决此问题。

例3 王刚同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板,王刚同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费。(1)你知道王刚是怎样剪的吗？用虚线表示出剪刀线；(2)请你画出王刚所拼的平行四边形。

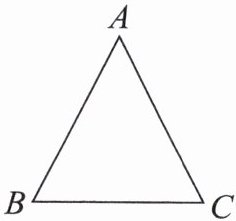
答案：
解析：这个问题要求同学们联系所学知识——平行四边形和三角形中位线进行多方面、多角度、多层次探究,它能检验大家思维的灵活性、发散性和创造性。
操作：如下图所示。