《2025年暑假生活指导八年级山东教育出版社》

8. 如图,$A$,$B$,$C$三点在数轴上,对应的数分别是$\frac{1}{x + 2}$,$1$,$\frac{3x}{2x + 4}$,且点$B到A$,$C$的距离相等,则$x = $____。

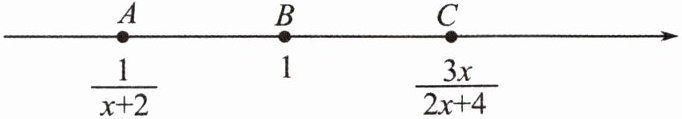
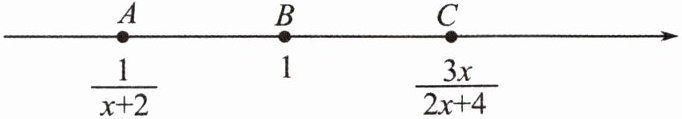
答案： 【解析】：
因为点$B$到点$A$和点$C$的距离相等，
所以点$B$是线段$AC$的中点，
即$B$对应的数是$A$和$C$对应数的平均值。
根据题意，点$A$、$B$、$C$在数轴上对应的数分别是$\frac{1}{x + 2}$，$1$，$\frac{3x}{2x + 4}$，
所以有$1=\frac{\frac{1}{x+2}+\frac{3x}{2x+4}}{2}$，
化简该等式：
$2=\frac{1}{x+2}+\frac{3x}{2x+4}$，
由于$2x+4=2(x+2)$，
所以$2=\frac{1}{x+2}+\frac{3x}{2(x+2)}$，
$2=\frac{2+3x}{2(x+2)}$，
交叉相乘得到：
$4(x+2)=2+3x$，
$4x+8=2+3x$，
$x=-6$。
经检验，$x=-6$是原方程的解。
【答案】：$-6$

9. 解关于$x的方程\frac{x}{x - 3}-2= \frac{m}{x - 3}$,得$x = 6 - m$。当$m = $____时,此根为增根,原方程无解；当$m\neq$____时,原方程有唯一解$x = 6 - m$。

答案： 【解析】：解关于$x$的方程$\frac{x}{x - 3} - 2 = \frac{m}{x - 3}$，首先方程两边同乘$x - 3$（$x\neq3$）去分母得：$x - 2(x - 3) = m$，去括号得$x - 2x + 6 = m$，合并同类项得$-x + 6 = m$，解得$x = 6 - m$。
因为原方程的分母为$x - 3$，所以增根是使分母为$0$的根，即$x = 3$。当$x = 3$时，代入$x = 6 - m$可得$3 = 6 - m$，解得$m = 3$，此时方程有增根，原方程无解。
当$m\neq3$时，$x = 6 - m$不会使分母为$0$，原方程有唯一解$x = 6 - m$。
【答案】：3；3

10. 等腰三角形一腰上的高与另一腰的夹角为$36^{\circ}$,则该等腰三角形的底角的度数为____。

答案： 【解析】：
当等腰三角形为锐角三角形时，此时腰上的高在三角形内部。
由题意知，一腰上的高与另一腰的夹角为$36^{\circ}$，那么顶角为：
$90^{\circ} - 36^{\circ} = 54^{\circ}$
由于是等腰三角形，底角相等，设底角为$\alpha$，则有：
$54^{\circ} + 2\alpha = 180^{\circ}$
解得：
$\alpha = \frac{180^{\circ} - 54^{\circ}}{2} = 63^{\circ}$
当等腰三角形为钝角三角形时，此时腰上的高在三角形外部。
由题意知，一腰上的高与另一腰的夹角的外角为$36^{\circ}$，那么顶角的外角为：
$90^{\circ} - 36^{\circ} = 54^{\circ}$
从而顶角为：
$180^{\circ} - 54^{\circ} = 126^{\circ}$
同样，由于是等腰三角形，底角相等，设底角为$\beta$，则有：
$126^{\circ} + 2\beta = 180^{\circ}$
解得：
$\beta = \frac{180^{\circ} - 126^{\circ}}{2} = 27^{\circ}$
综上所述，等腰三角形的底角度数为$63^{\circ}$或$27^{\circ}$。
【答案】：$63^{\circ}$或$27^{\circ}$

11. 已知$\angle AOB = 60^{\circ}$,点$P是\angle AOB的平分线OC$上的动点,点$M在边OA$上,且$OM = 4$,则点$P到点M与到边OA$的距离之和的最小值是____。

答案： 【解析】：过点M作OA的垂线，交OC于点P，此时点P到点M与到边OA的距离之和最小。因为OC是∠AOB的平分线，∠AOB=60°，所以∠AOC=30°。在直角三角形POM中，OM=4，∠POM=30°，点P到OA的距离即为PM在OA上的高，设点P到OA的距离为h，根据三角函数关系，h=PM·sin30°，而此时PM的长度等于点P到M的距离，所以距离之和为PM + h = PM + PM·sin30° = PM·(1 + 0.5) = 1.5PM。又因为在直角三角形中，sin30° = h / OP，cos30° = OM / OP，所以OP = OM / cos30° = 4 / (√3/2) = 8√3/3，h = OP·sin30° = 8√3/3 × 1/2 = 4√3/3，而PM = √(OM² - h²)（此处错误，应为PM = h / sin30° = 2h，因为h = PM·sin30°），所以PM = 2h，距离之和为PM + h = 3h，又因为h = OP·sin30°，OP·cos30° = OM = 4，所以OP = 4 / cos30°，h = 4 / cos30° × sin30° = 4tan30° = 4×(√3/3) = 4√3/3，所以距离之和为3h = 3×4√3/3 = 4√3。但更简便的是，作点M关于OC的对称点M'，则点M'在OB上，且OM'=OM=4，点P到OA的距离等于点P到OB的距离，所以点P到点M与到边OA的距离之和等于点P到点M与到边OB的距离之和，即PM + PD（D为P到OB的垂足），当M'、P、D三点共线且M'D⊥OB时，距离之和最小，此时M'D的长度即为最小值，在直角三角形OM'D中，∠M'OD=60°，OM'=4，所以M'D=OM'·sin60°=4×(√3/2)=2√3。
【答案】：2√3

1. 若$x\gt y$,则下列式子错误的是( )。

A.$x - 3\gt y - 3$
B.$-3x\gt -3y$
C.$x + 3\gt y + 3$
D.$\frac{x}{3}\gt\frac{y}{3}$

答案： 【解析】：
A选项：对于$x - 3 \gt y - 3$，由于两边同时减去相同的数3，不改变不等式的方向，所以A选项是正确的。
B选项：对于$-3x \gt -3y$，当两边同时乘以一个负数时，不等式的方向会反转。原不等式$x \gt y$两边同时乘以-3，应得到$-3x \lt -3y$，所以B选项是错误的。
C选项：对于$x + 3 \gt y + 3$，由于两边同时加上相同的数3，不改变不等式的方向，所以C选项是正确的。
D选项：对于$\frac{x}{3} \gt \frac{y}{3}$，由于两边同时除以一个正数3，不改变不等式的方向，所以D选项是正确的。
综上所述，错误的选项是B。
【答案】：B

2. 若分式$\frac{3x - 6}{2x + 1}的值为0$,则( )。

A.$x = -2$
B.$x = -\frac{1}{2}$
C.$x = \frac{1}{2}$
D.$x = 2$

答案： 【解析】：要使分式$\frac{3x - 6}{2x + 1}$的值为0，必须满足分子为0且分母不为0。
首先，令分子为0，即$3x - 6 = 0$，解得$x = 2$。
然后，检查分母是否为0，当$x = 2$时，分母$2x + 1 = 2 × 2 + 1 = 5 \neq 0$。
因此，当$x = 2$时，分式的值为0。
【答案】：D

3. 化简$(x-\frac{2x - 1}{x})÷(1-\frac{1}{x})$的结果是( )。

A.$\frac{1}{x}$
B.$x - 1$
C.$\frac{x - 1}{x}$
D.$\frac{x - 1}{x}$

答案： 【解析】：
首先，处理被除数部分：
$x - \frac{2x - 1}{x} = \frac{x^2}{x} - \frac{2x - 1}{x} = \frac{x^2 - 2x + 1}{x} = \frac{(x - 1)^2}{x}$
然后，处理除数部分：
$1 - \frac{1}{x} = \frac{x}{x} - \frac{1}{x} = \frac{x - 1}{x}$
接着，进行除法运算：
$\frac{(x - 1)^2}{x} ÷ \frac{x - 1}{x} = \frac{(x - 1)^2}{x} \cdot \frac{x}{x - 1} = x - 1$
【答案】：B

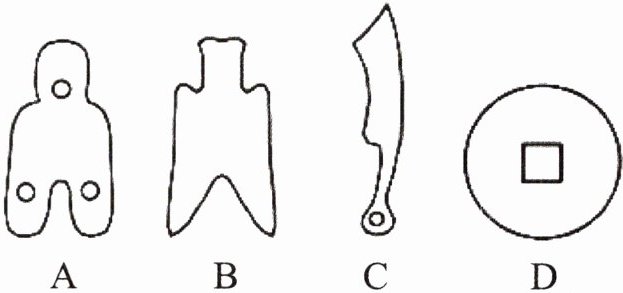
4. 古钱币是我国悠久的历史文化遗产,以下是在《中国古代钱币》特种邮票中选取的部分图形,其中既是轴对称图形又是中心对称图形的是( )。

答案： 【解析】：
轴对称图形是指图形关于某条直线（轴）对称，即图形上的每一点关于这条轴的对称点都在图形上。
中心对称图形是指图形关于某一点（中心）对称，即图形上的每一点关于这个中心的对称点都在图形上。
A选项（布币）：布币的形状并不关于某条直线或某点对称，所以它不是轴对称图形，也不是中心对称图形。
B选项（刀币）：刀币的形状同样不关于某条直线或某点对称，所以它不是轴对称图形，也不是中心对称图形。
C选项（尖型币）：尖型币的形状也不关于某条直线或某点对称，所以它不是轴对称图形，也不是中心对称图形。
D选项（圆形方孔钱）：圆形方孔钱的形状关于其圆心中心对称，同时也关于过圆心的任意直线轴对称。因此，它既是轴对称图形，也是中心对称图形。
【答案】：D

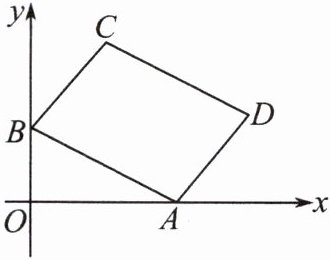
5. 如图,四边形$ABCD$是平行四边形,点$A$,$B$,$C的坐标分别为(2,0)$,$(0,1)$,$(1,2)$,则$AB + BC$的值为( )。


A.$\sqrt{5}+\sqrt{2}$
B.$3$
C.$4$
D.$5$

答案： 【解析】：已知四边形$ABCD$是平行四边形，点$A(2,0)$，$B(0,1)$，$C(1,2)$。根据平行四边形的性质，对边相等，所以$AB = CD$，$BC = AD$，但题目要求的是$AB + BC$，因此需要分别计算$AB$和$BC$的长度。
计算$AB$的长度：
点$A(2,0)$和点$B(0,1)$之间的距离，根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$：
$AB = \sqrt{(0 - 2)^2 + (1 - 0)^2} = \sqrt{(-2)^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}$
计算$BC$的长度：
点$B(0,1)$和点$C(1,2)$之间的距离：
$BC = \sqrt{(1 - 0)^2 + (2 - 1)^2} = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2}$
计算$AB + BC$：
$AB + BC = \sqrt{5} + \sqrt{2}$
【答案】：A

6. 如图,在$□ ABCD$中,用直尺和圆规作$\angle BAD的平分线AG$,若$AD = 5$,$DE = 6$,则$AG$的长是( )。


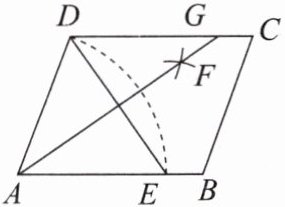
A.$6$
B.$8$
C.$10$
D.$12$

答案： 【解析】：在平行四边形$ABCD$中，$AD// BC$，$AB// CD$，$AD = BC = 5$，$AB = CD$。
因为$AG$是$\angle BAD$的平分线，所以$\angle BAG=\angle DAG$。
又因为$AD// BC$，所以$\angle DAG = \angle AGB$（两直线平行，内错角相等），因此$\angle BAG=\angle AGB$，所以$\triangle ABG$是等腰三角形，$AB = BG$。
设$AB = BG = x$，则$CG=BC - BG=5 - x$。
由作图可知，$AE = AD = 5$（圆规作图，以$A$为圆心，$AD$长为半径画弧交$AB$于$E$），$DG = DE = 6$（以$D$、$E$为圆心，大于$\frac{1}{2}DE$长为半径画弧，两弧交于$F$，作直线$AF$即$AG$，所以$AG$垂直平分$DE$，故$DG = EG = 6$）。
因为$AB// CD$，所以$\triangle AEF\sim\triangle DGF$（此处$F$为$AG$与$DE$的交点），但更简便的是在$\triangle ADE$中，$AG$垂直平分$DE$，设$AG$与$DE$交于点$O$，则$DO = OE=\frac{DE}{2}=3$，$AO\perp DE$。
在$Rt\triangle AOD$中，$AD = 5$，$DO = 3$，根据勾股定理可得$AO=\sqrt{AD^{2}-DO^{2}}=\sqrt{5^{2}-3^{2}} = 4$。
设$OG = y$，因为$AB// CD$，所以$\frac{AO}{OG}=\frac{AE}{DG}$（$AE = AB = x$，$DG = 6$，$AE// DG$，所以$\triangle AOE\sim\triangle GOD$），即$\frac{4}{y}=\frac{x}{6}$，$x=\frac{24}{y}$。
又因为$BG = x$，$AD = BC = 5$，$CG = CD - DG = x - 6$（因为$CD = AB = x$），而$BC = BG + CG$，所以$5=x+(x - 6)$，解得$2x=11$，$x = 5.5$？此思路有误，应利用平行四边形对边相等$AB = CD$，$CD = CG + DG$，$CG = BG - BC$表述错误，正确的是$BG = AB = x$，$AD = BC = 5$，$CG = BC - BG = 5 - x$，而$CD = AB = x$，所以$CD = CG + DG$，即$x=(5 - x)+6$，解得$2x=11$，$x = 5.5$，此结果与前面$AO = 4$结合，在$\triangle GOE$中，$OE = 3$，$EG = 6$，则$OG=\sqrt{EG^{2}-OE^{2}}=\sqrt{6^{2}-3^{2}} = 3\sqrt{3}$，显然矛盾，说明前面“$DG = DE = 6$”错误。
正确作图分析：以$A$为圆心，$AD$为半径画弧交$AB$于$E$，所以$AE = AD = 5$；以$D$、$E$为圆心，大于$\frac{1}{2}DE$为半径画弧交于两点，过两点的直线即$AG$，所以$AG$是$DE$的垂直平分线，设垂足为$O$，则$DO = OE=\frac{DE}{2}=3$，$AG\perp DE$。
在$Rt\triangle AOE$中，$AE = 5$，$OE = 3$，则$AO=\sqrt{AE^{2}-OE^{2}}=\sqrt{5^{2}-3^{2}} = 4$。
因为$ABCD$是平行四边形，所以$AD// BC$，所以$\angle DAG=\angle AGB$，又$\angle DAG=\angle BAG$，所以$\angle BAG=\angle AGB$，故$AB = BG$。
设$AB = BG = x$，则$EB = AB - AE = x - 5$。
因为$AD// BC$，所以$\triangle AOD\sim\triangle GOB$（$O$为$AG$与$DE$交点），$\frac{AO}{OG}=\frac{AD}{BG}=\frac{DO}{BO}$，即$\frac{4}{OG}=\frac{5}{x}$，所以$OG=\frac{4x}{5}$。
又因为$DE = 6$，在$\triangle DEB$中，$AG$垂直平分$DE$，但$EB = x - 5$，$DG = EG$（垂直平分线上的点到两端距离相等），$DG = DC - CG = x - (BC - BG)=x - (5 - x)=2x - 5$，$EG = EB + BG$？不对，$E$在$AB$上，$G$在$CD$上，连接$EG$、$DG$，则$DG = EG$，在$\triangle DGC$和$\triangle EGB$中，$DC// AB$，$\angle DGO=\angle EGO$（$OG$为角平分线），但用坐标法更清晰：
设$O$为原点$(0,0)$，$DE$在$x$轴上，$D(-3,0)$，$E(3,0)$，$AG$在$y$轴上，$A(0,4)$（因为$AO = 4$）。
则$AD$的斜率$k_{AD}=\frac{0 - 4}{-3 - 0}=\frac{4}{3}$，因为$AD// BC$，$AB// CD$，$A(0,4)$，$E(3,0)$在$AB$上，所以直线$AB$过$A(0,4)$和$E(3,0)$，斜率$k_{AB}=\frac{0 - 4}{3 - 0}=-\frac{4}{3}$，方程为$y=-\frac{4}{3}x + 4$。
直线$AD$：过$A(0,4)$，斜率$\frac{4}{3}$，方程为$y=\frac{4}{3}x + 4$，$D(-3,0)$在其上。
$G$在$AG$（$y$轴，$x = 0$）上，设$G(0,g)$，因为$G$在$CD$上，$CD// AB$，斜率为$-\frac{4}{3}$，过$D(-3,0)$，所以直线$CD$方程：$y - 0=-\frac{4}{3}(x + 3)$，即$y=-\frac{4}{3}x - 4$，$G(0,g)$在$CD$上，所以$g=-\frac{4}{3}×0 - 4=-4$，即$G(0,-4)$。
所以$AG$的长为$A(0,4)$到$G(0,-4)$的距离，即$|4 - (-4)|=8$。
【答案】：B