《2025年暑假生活指导八年级山东教育出版社》

1. 解不等式组：$\left\{\begin{array}{l}2(x + 2)\gt x + 3①,\frac{x}{3}\lt\frac{x + 2}{5}②,\end{array} \right.$并写出它的所有整数解。

答案： 【解析】：
首先解不等式①：$2(x + 2) \gt x + 3$，
展开得：$2x + 4 \gt x + 3$，
移项得：$x \gt -1$。
然后解不等式②：$\frac{x}{3} \lt \frac{x + 2}{5}$，
两边同时乘以15（最小公倍数）消去分母得：$5x \lt 3x + 6$，
移项得：$2x \lt 6$，
除以2得：$x \lt 3$。
综合不等式①和不等式②的解集，我们得到不等式组的解集为：$-1 \lt x \lt 3$。
在这个范围内，不等式组的所有整数解为：$0, 1, 2$。
【答案】：
$0, 1, 2$

2. 计算：$(\frac{3x}{x - 1}-\frac{x}{x + 1})\cdot\frac{x^{2}-1}{2x}$。

答案： 【解析】：
首先，将两个分数进行通分，通分母为 $(x - 1)(x + 1)$。
$\frac{3x}{x - 1} - \frac{x}{x + 1} = \frac{3x(x + 1) - x(x - 1)}{(x - 1)(x + 1)}$，
然后对分子进行展开和合并同类项，
原式变为：$\frac{3x^2 + 3x - x^2 + x}{(x - 1)(x + 1)} = \frac{2x^2 + 4x}{(x - 1)(x + 1)}$，
接着，我们将这个结果与 $\frac{x^2 - 1}{2x}$ 相乘，
注意到 $x^2 - 1$ 可以分解为 $(x - 1)(x + 1)$，
这样我们就可以进行约分，
原式变为：$\frac{2x^2 + 4x}{(x - 1)(x + 1)} \cdot \frac{(x - 1)(x + 1)}{2x}$，
约分后，我们得到：$\frac{2x^2 + 4x}{2x} = x + 2$。
【答案】：$x + 2$

3. 解方程：$\frac{x - 3}{x - 2}+1= \frac{3}{2 - x}$。

答案： 【解析】：方程两边同乘$x - 2$，得$x - 3 + (x - 2) = -3$，去括号得$x - 3 + x - 2 = -3$，移项合并同类项得$2x = 2$，解得$x = 1$。检验：当$x = 1$时，$x - 2 = -1 \neq 0$，所以原分式方程的解为$x = 1$。
【答案】：$x = 1$

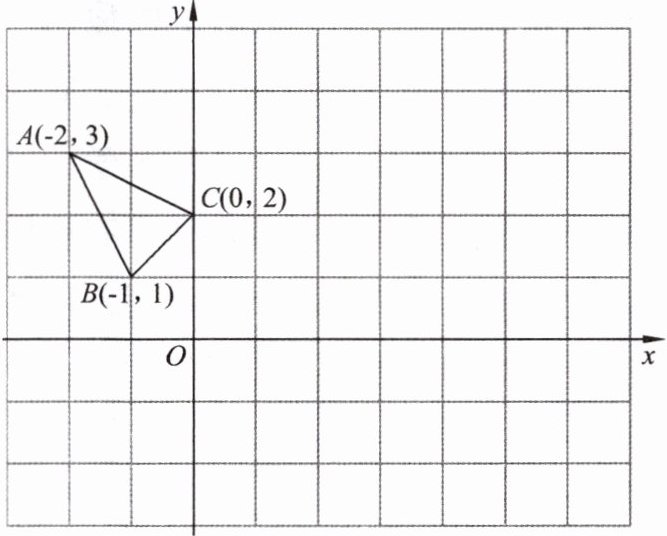
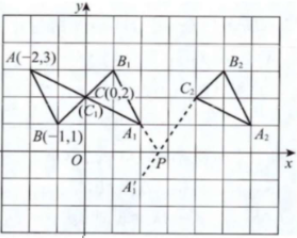
4. $\triangle ABC在平面直角坐标系xOy$中的位置如图所示。(1)作$\triangle ABC关于点C成中心对称的\triangle A_{1}B_{1}C_{1}$；(2)将$\triangle A_{1}B_{1}C_{1}$向右平移4个单位长度,作出平移后的$\triangle A_{2}B_{2}C_{2}$；(3)在$x轴上求作一点P$,使$PA_{1}+PC_{2}$的值最小,并写出点$P$的坐标。(不写解答过程,直接写出结果)

答案：

5. 某校开设智能机器人编程的校本课程,购买了$A$、$B$两种型号的机器人模型。$A型机器人模型单价比B$型机器人模型单价多200元,用2000元购买$A$型机器人模型和用1200元购买$B$型机器人模型的数量相同。求$A$、$B$两种型号的机器人模型的单价分别是多少元。

答案： 【解析】：
设A型机器人模型的单价为$x$元，B型机器人模型的单价为$y$元。
根据题意，可以列出以下两个方程：
1. $x = y + 200$
2. $\frac{2000}{x} = \frac{1200}{y}$
从第一个方程中，我们可以得到：
$x - y = 200$
将第一个方程代入第二个方程中，得到：
$\frac{2000}{y + 200} = \frac{1200}{y}$
交叉相乘，得到：
$2000y = 1200(y + 200)$
展开并整理，得到：
$2000y = 1200y + 240000$
进一步整理，得到：
$800y = 240000$
解得：
$y = 300$
将$y = 300$代入第一个方程，得到：
$x = 300 + 200 = 500$
所以，A型机器人模型的单价为500元，B型机器人模型的单价为300元。
【答案】：
A型机器人模型单价为500元，B型机器人模型单价为300元。

6. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 32^{\circ}$,以直角顶点$C$为旋转中心,将$\triangle ABC旋转到\triangle A'B'C$的位置,其中$A'$,$B'分别是A$,$B$的对应点,且点$B在斜边A'B'$上,直角边$CA'交AB于D$,求$\angle BDC$的度数。

答案： 【解析】：在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$\angle A = 32^{\circ}$，根据三角形内角和定理，$\angle ABC=180^{\circ}-\angle ACB-\angle A=180^{\circ}-90^{\circ}-32^{\circ}=58^{\circ}$。
因为以点$C$为旋转中心将$\triangle ABC$旋转到$\triangle A'B'C$的位置，所以旋转角$\angle ACA'=\angle BCB'$，且$CB=CB'$，$\angle A'=\angle A = 32^{\circ}$，$\angle A'B'C=\angle ABC = 58^{\circ}$。
由于$CB=CB'$，所以$\triangle CBB'$是等腰三角形，$\angle CBB'=\angle CB'B$。又因为点$B$在斜边$A'B'$上，所以$\angle A'B'C=\angle CB'B = 58^{\circ}$，那么在$\triangle CBB'$中，$\angle BCB'=180^{\circ}-2\angle CB'B=180^{\circ}-2×58^{\circ}=64^{\circ}$，即旋转角$\angle ACA' = 64^{\circ}$。
在$\triangle ADC$中，$\angle A = 32^{\circ}$，$\angle ACD=\angle ACA' = 64^{\circ}$，所以$\angle ADC=180^{\circ}-\angle A-\angle ACD=180^{\circ}-32^{\circ}-64^{\circ}=84^{\circ}$。
因为$\angle BDC$与$\angle ADC$是邻补角，所以$\angle BDC=180^{\circ}-\angle ADC=180^{\circ}-84^{\circ}=96^{\circ}$。
【答案】：96°