《2025年智趣暑假作业八年级数学人教版》

2. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,$AC= 3$,$BC= 4$,以点$A$为圆心,$AC$长为半径画弧,交$AB于点D$,则$BD= $2.

答案： 解：在$Rt△ABC$中，$∠C=90^{\circ}$，$AC=3$，$BC=4$，
由勾股定理得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}}=5$。
因为以点$A$为圆心，$AC$长为半径画弧交$AB$于点$D$，所以$AD=AC=3$。
则$BD=AB - AD=5 - 3=2$。
2

3. 若直角三角形的两直角边长分别为$a$,$b$,且满足$\sqrt {a^{2}-6a+9}+|b-4|= 0$,则该直角三角形的斜边长为5.

答案： 解：因为$\sqrt{a^2 - 6a + 9} + |b - 4| = 0$，$\sqrt{a^2 - 6a + 9} = \sqrt{(a - 3)^2} \geq 0$，$|b - 4| \geq 0$，所以$\sqrt{(a - 3)^2} = 0$，$|b - 4| = 0$，即$a - 3 = 0$，$b - 4 = 0$，解得$a = 3$，$b = 4$。
由勾股定理得斜边长为$\sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = 5$。
5

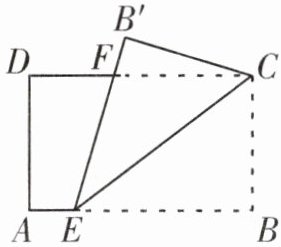
1. 如图,将长方形纸片沿着$CE$所在的直线折叠,$B点落在点B'$处,$CD与EB'相交于点F$,如果$AB= 10cm$,$AD= 6cm$,$AE= 2cm$,求$EF$的长.

答案： 解：
∵ 四边形 $ABCD$ 是长方形，
∴ $AB=CD=10\,\text{cm}$，$AD=BC=6\,\text{cm}$，$\angle A=\angle B=\angle D=90^\circ$。
∵ $AE=2\,\text{cm}$，
∴ $EB=AB-AE=10-2=8\,\text{cm}$。
由折叠性质得：$EB'=EB=8\,\text{cm}$，$\angle B'=\angle B=90^\circ$，$CB'=CB=6\,\text{cm}$。
设 $EF=x\,\text{cm}$，则 $FB'=EB'-EF=8-x\,\text{cm}$。
∵ $\angle DFE=\angle B'FC$，$\angle D=\angle B'=90^\circ$，
∴ $\triangle DFE \sim \triangle B'FC$。
∴ $\frac{DF}{B'F}=\frac{DE}{B'C}$。
∵ $DE=AD=6\,\text{cm}$，$B'C=6\,\text{cm}$，
∴ $\frac{DF}{8-x}=\frac{6}{6}=1$，即 $DF=8-x$。
∵ $DF+FC=CD=10\,\text{cm}$，
∴ $FC=10-DF=10-(8-x)=x+2$。
在 $\text{Rt}\triangle B'FC$ 中，由勾股定理得：
$FB'^2 + B'C^2 = FC^2$，
即 $(8-x)^2 + 6^2 = (x+2)^2$。
解得 $x=\frac{25}{4}$。
∴ $EF=\frac{25}{4}\,\text{cm}$。
$\boxed{\frac{25}{4}}$

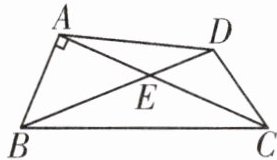
2. 如图,在四边形$ABCD$中,对角线$AC$,$BD交于点E$,$∠BAC= 90^{\circ }$,$∠CED= 45^{\circ }$,$∠DCE= 30^{\circ }$,$DE= \sqrt {2}$,$BE= 2\sqrt {2}$,求$CD的长和四边形ABCD$的面积.

答案： 解：过点 D 作 DF⊥AC 于点 F。
在 Rt△DFE 中，∠CED=45°，DE=√2，
∴DF=EF=DE·sin45°=√2×√2/2=1。
在 Rt△DFC 中，∠DCE=30°，DF=1，
∴CD=2DF=2，CF=DF·cot30°=1×√3=√3。
设 AE=x，∠BAC=90°，∠AEB=∠CED=45°，
∴AB=AE=x，BE=√2x。
∵BE=2√2，
∴√2x=2√2，解得 x=2，即 AE=AB=2。
AC=AE+EF+FC=2+1+√3=3+√3。
S△ABC=1/2×AB×AC=1/2×2×(3+√3)=3+√3。
S△ADC=1/2×AC×DF=1/2×(3+√3)×1=(3+√3)/2。
S四边形ABCD=S△ABC+S△ADC=3+√3+(3+√3)/2=(6+2√3+3+√3)/2=(9+3√3)/2= (3√3 + 9)/2。
CD 的长为 2，四边形 ABCD 的面积是 (3√3 + 9)/2。