《2025年智趣暑假作业八年级数学人教版》

1. 在$△ABC$中,三边长a,b,c满足$a^{2}+b^{2}= 25,a^{2}-b^{2}= 7,c= 5$,则最大边上的高为$\frac{12}{5}$.

答案： 解：联立方程$\begin{cases}a^{2}+b^{2}=25\\a^{2}-b^{2}=7\end{cases}$，两式相加得$2a^{2}=32$，解得$a^{2}=16$，则$a = 4$（边长为正）。将$a^{2}=16$代入$a^{2}+b^{2}=25$，得$b^{2}=9$，$b = 3$。
因为$a^{2}+b^{2}=16 + 9=25=c^{2}$，所以$\triangle ABC$是直角三角形，$c$为斜边（最大边）。
设斜边上的高为$h$，根据面积相等，$\frac{1}{2}ab=\frac{1}{2}ch$，即$\frac{1}{2}×4×3=\frac{1}{2}×5h$，解得$h=\frac{12}{5}$。
$\frac{12}{5}$

2. 如图,已知在$Rt△ABC$中,$∠ACB= 90^{\circ },AB= 4$,分别以AC,BC长为直径作半圆,面积分别记为$S_{1},S_{2}$,则$S_{1}+S_{2}$的值等于____2π.

答案： 解：设AC = a，BC = b。
在Rt△ABC中，∠ACB = 90°，AB = 4，由勾股定理得：a² + b² = AB² = 16。
S₁为以AC为直径的半圆面积，S₁ = ½π(½a)² = ⅛πa²。
S₂为以BC为直径的半圆面积，S₂ = ½π(½b)² = ⅛πb²。
S₁ + S₂ = ⅛πa² + ⅛πb² = ⅛π(a² + b²) = ⅛π×16 = 2π。
答案：2π

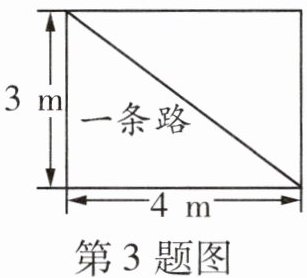
3. 如图所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”. 他们仅仅少走了4步路(假设2步为1m),踩伤了花草.

答案： 解：由图可知，长方形花圃的长为4m，宽为3m。
走拐角的路程为：3 + 4 = 7m
走“捷径”的路程为直角三角形斜边，根据勾股定理：
斜边长度 = √(3² + 4²) = √(9 + 16) = √25 = 5m
少走的路程为：7 - 5 = 2m
因为2步为1m，所以少走的步数为：2 × 2 = 4步
答案：4

三、解答题
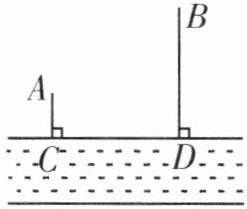
如图,A,B两个小镇在河岸CD的同侧,到河岸的距离分别为$AC= 10$千米,$BD= $30千米,且$CD= 30$千米,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河岸CD上选择水厂的位置E,使铺设水管的费用最节省,并求出总费用.

答案： 解：作点A关于河岸CD的对称点$A'$，连接$BA'$，与CD交于点E，则点E即为所求水厂位置。
过点$A'$作$A'F \perp BD$交BD的延长线于点F，由对称性可知$A'C=AC=10$千米，所以$A'F=CD=30$千米，$BF=BD+A'C=30+10=40$千米。
在$Rt\triangle A'FB$中，根据勾股定理可得$BA'=\sqrt{A'F^{2}+BF^{2}}=\sqrt{30^{2}+40^{2}}=50$千米，即$AE+BE=50$千米。
总费用为$50×3=150$万元。
答：总费用为150万元。