2025年智趣暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智趣暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 已知菱形的周长为24 cm,两邻角之比为$2:1$,则较短的对角线的长为
6 cm
.
答案:
解:
∵菱形周长为24 cm,
∴菱形边长为 $24 ÷ 4 = 6$ cm.
∵菱形两邻角之和为180°,且两邻角之比为2:1,
∴较小内角为 $180^\circ × \frac{1}{2+1} = 60^\circ$.
∵菱形四边相等,较小内角为60°,
∴较短对角线与两边构成等边三角形,
∴较短对角线长等于边长,即6 cm.
答案:6 cm
∵菱形周长为24 cm,
∴菱形边长为 $24 ÷ 4 = 6$ cm.
∵菱形两邻角之和为180°,且两邻角之比为2:1,
∴较小内角为 $180^\circ × \frac{1}{2+1} = 60^\circ$.
∵菱形四边相等,较小内角为60°,
∴较短对角线与两边构成等边三角形,
∴较短对角线长等于边长,即6 cm.
答案:6 cm
3. 如图,四边形ABCD是菱形,点O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分,当菱形的两条对角线的长分别为6和8时,阴影部分的面积为
12
.
答案:
解:
∵菱形的两条对角线长分别为6和8,
∴菱形面积为 $\frac{1}{2} × 6 × 8 = 24$。
∵菱形的对角线互相平分,过对角线交点O的直线将菱形面积平分,
∴阴影部分面积为菱形面积的一半,即 $\frac{1}{2} × 24 = 12$。
12
∵菱形的两条对角线长分别为6和8,
∴菱形面积为 $\frac{1}{2} × 6 × 8 = 24$。
∵菱形的对角线互相平分,过对角线交点O的直线将菱形面积平分,
∴阴影部分面积为菱形面积的一半,即 $\frac{1}{2} × 24 = 12$。
12
1. 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过点M作$ME⊥CD$于点E,$∠1= ∠2$.
(1)若$CE= 1$,求BC的长;
(2)求证:$AM= DF+ME$.
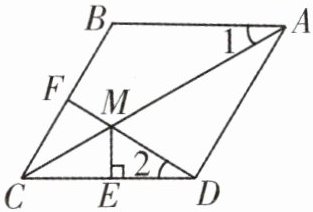
(1)若$CE= 1$,求BC的长;
(2)求证:$AM= DF+ME$.

答案:
(1)解:
∵四边形ABCD是菱形,
∴BC=CD,AB//CD,
∴∠1=∠ACD。
∵∠1=∠2,
∴∠ACD=∠2,
∴MC=MD。
∵ME⊥CD,
∴CE=DE=1,
∴CD=CE+DE=2,
∴BC=CD=2。
(2)证明:延长DF至点G,使FG=ME,连接CG。
∵F为BC中点,
∴BF=CF。
∵AB//CD,
∴∠1=∠ACD=∠2,∠CMF=∠AMD。
在△CME和△CDG中,∠MCE=∠DCG,MC=MD,∠CME=∠CDG,
∴△CME≌△CDG(ASA),
∴ME=DG,CG=CE。
∵AB=CD,∠B=∠DCB,BF=CF,
∴△ABF≌△DCF(SAS),
∴AF=DF。
∵∠GCF=∠2+∠MCG=∠1+∠MCE=∠ACB,
∴∠ACG=∠ACB+∠BCG=∠GCF+∠BCG=∠BCF=∠BAC,
∴AG=CG=CE=DE。
∵AM=AG+GM,GM=DF,AG=ME,
∴AM=DF+ME。
(1)解:
∵四边形ABCD是菱形,
∴BC=CD,AB//CD,
∴∠1=∠ACD。
∵∠1=∠2,
∴∠ACD=∠2,
∴MC=MD。
∵ME⊥CD,
∴CE=DE=1,
∴CD=CE+DE=2,
∴BC=CD=2。
(2)证明:延长DF至点G,使FG=ME,连接CG。
∵F为BC中点,
∴BF=CF。
∵AB//CD,
∴∠1=∠ACD=∠2,∠CMF=∠AMD。
在△CME和△CDG中,∠MCE=∠DCG,MC=MD,∠CME=∠CDG,
∴△CME≌△CDG(ASA),
∴ME=DG,CG=CE。
∵AB=CD,∠B=∠DCB,BF=CF,
∴△ABF≌△DCF(SAS),
∴AF=DF。
∵∠GCF=∠2+∠MCG=∠1+∠MCE=∠ACB,
∴∠ACG=∠ACB+∠BCG=∠GCF+∠BCG=∠BCF=∠BAC,
∴AG=CG=CE=DE。
∵AM=AG+GM,GM=DF,AG=ME,
∴AM=DF+ME。
2. 如图,在四边形ABCD中,$AB= CD$,M,N,P,Q分别是AD,BC,BD,AC的中点,连接MN,PQ,请你探索MN与PQ的关系,并证明你的结论.


答案:
解:MN与PQ的关系是MN⊥PQ且MN=PQ。
证明:连接MP,PN,NQ,QM。
∵M,P分别是AD,BD的中点,
∴MP是△ABD的中位线,
∴MP=$\frac{1}{2}$AB,MP//AB。
同理,NQ=$\frac{1}{2}$AB,NQ//AB,
∴MP=NQ,MP//NQ,
∴四边形MPNQ是平行四边形。
∵P,N分别是BD,BC的中点,
∴PN是△BCD的中位线,
∴PN=$\frac{1}{2}$CD。
∵AB=CD,
∴MP=PN,
∴平行四边形MPNQ是菱形,
∴MN⊥PQ,MN=PQ。
综上,MN与PQ垂直且相等。
证明:连接MP,PN,NQ,QM。
∵M,P分别是AD,BD的中点,
∴MP是△ABD的中位线,
∴MP=$\frac{1}{2}$AB,MP//AB。
同理,NQ=$\frac{1}{2}$AB,NQ//AB,
∴MP=NQ,MP//NQ,
∴四边形MPNQ是平行四边形。
∵P,N分别是BD,BC的中点,
∴PN是△BCD的中位线,
∴PN=$\frac{1}{2}$CD。
∵AB=CD,
∴MP=PN,
∴平行四边形MPNQ是菱形,
∴MN⊥PQ,MN=PQ。
综上,MN与PQ垂直且相等。
查看更多完整答案,请扫码查看


