《2025年智趣暑假作业八年级数学人教版》

1. 如图,在平面直角坐标系中,菱形OABC的顶点C的坐标是$(3,4)$,则顶点A,B的坐标分别是(D)
A.$(4,0),(7,4)$
B.$(4,0),(8,4)$
C.$(5,0),(7,4)$
D.$(5,0),(8,4)$

答案： 解：
∵ 菱形OABC中，点C坐标为(3,4)，
∴ OC = √(3² + 4²) = 5，即菱形边长为5。
∵ OA = OC = 5，且点A在x轴上，
∴ A点坐标为(5,0)。
∵ BC = OA = 5，BC//OA，点C坐标为(3,4)，
∴ B点横坐标为3 + 5 = 8，纵坐标与C相同为4，即B(8,4)。
答案：D

2. 如图,菱形ABCD的两条对角线相交于O,若$AC= 6$,$BD= 4$,则菱形ABCD的周长是(C)
A.24
B.16
C.$4\sqrt {13}$
D.$2\sqrt {3}$

答案： 解：
∵菱形ABCD的对角线AC=6，BD=4，且相交于点O，
∴AC⊥BD，AO=AC/2=3，BO=BD/2=2。
在Rt△AOB中，由勾股定理得：
AB=√(AO²+BO²)=√(3²+2²)=√13。
∵菱形四边相等，
∴周长=4AB=4√13。
答案：C

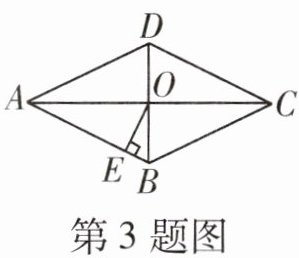
3. 如图,在菱形ABCD中,对角线AC与BD相交于点O,$OE⊥AB$,垂足为E,若$∠ADC= 130^{\circ }$,则$∠AOE$的大小为(B)

A.$75^{\circ }$
B.$65^{\circ }$
C.$55^{\circ }$
D.$50^{\circ }$

答案： 解：
∵四边形ABCD是菱形，∠ADC=130°，
∴AD//BC，∠ABC=∠ADC=130°，
∠OAB=∠OAD，AC⊥BD（菱形对角线互相垂直平分且平分内角），
∴∠DAB=180°-∠ADC=50°（两直线平行，同旁内角互补），
∴∠OAB=1/2∠DAB=25°，
∵OE⊥AB，
∴∠OEA=90°，
在Rt△AOE中，∠AOE=90°-∠OAB=90°-25°=65°．
答案：B

4. 如图,在$□ ABCD$中,AE,CF分别是$∠BAD和∠BCD$的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是(C)
A.$AE= AF$
B.$EF⊥AC$
C.$∠B= 60^{\circ }$
D.AC是$∠EAF$的平分线

答案： 解：
在$□ABCD$中，$AD// BC$，$∠BAD=∠BCD$，$AB=CD$，$AD=BC$。
$∵AE$，$CF$分别平分$∠BAD$和$∠BCD$，
$∴∠BAE=∠DAE=\frac{1}{2}∠BAD$，$∠DCF=∠BCF=\frac{1}{2}∠BCD$，
$∴∠DAE=∠BCF$。
又$∵AD// BC$，$∴∠DAE=∠AEB$，$∴∠AEB=∠BCF$，$∴AE// CF$。
同理可证$AF// EC$，$∴$四边形$AECF$是平行四边形。
A. 若$AE=AF$，则平行四边形$AECF$是菱形；
B. 若$EF⊥AC$，则平行四边形$AECF$是菱形；
C. 若$∠B=60^{\circ}$，无法判定平行四边形$AECF$是菱形；
D. 若$AC$平分$∠EAF$，则$∠EAC=∠FAC$，
$∵AD// BC$，$∴∠FAC=∠ACE$，$∠EAC=∠AEC$，
$∴∠AEC=∠ACE$，$∴AE=CE$，则平行四边形$AECF$是菱形。
答案：C

1. 如图,在平行四边形ABCD中,因为$∠1= ∠2$,所以$BC= DC$,所以平行四边形ABCD是菱形,依据是有一组邻边相等的平行四边形是菱形.

答案： 解：有一组邻边相等的平行四边形是菱形