《2025年智趣暑假作业八年级数学人教版》

2. 已知,如图所示的图形的面积为 24,根据图中的条件,可列出方程:$x(x + 1) + x = 24$.

答案： 解：观察图形可知，该图形可看作一个边长为$x + 1$的大正方形减去右上角一个边长为$1$的小正方形（或看作一个长为$x + 1$、宽为$x$的长方形与一个长为$x$、宽为$1$的长方形组合）。
若看作组合图形，左边长方形面积为$x(x + 1)$，右边长方形面积为$x×1 = x$，总面积为$24$，则方程为$x(x + 1) + x = 24$。
$x(x + 1) + x = 24$

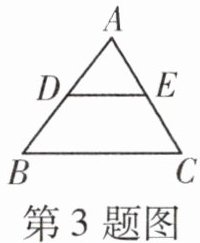
3. 如图所示,在$△ABC$中,点 D,E 分别是 AB,AC 的中点. 若$DE= 3$,则 BC= ____6.

答案： 解：
∵点D，E分别是AB，AC的中点
∴DE是△ABC的中位线
∵DE=3
∴BC=2DE=2×3=6
答案：6

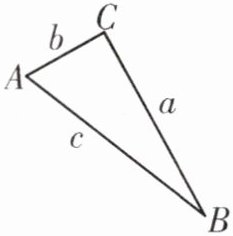
1. 如图,已知$△ABC$的三边长分别为a,b,c,且$a+b= 17,ab= 60,c= 13$,试判断$△ABC$的形状.

答案： 解：因为 $a + b = 17$，$ab = 60$，所以 $a^2 + b^2 = (a + b)^2 - 2ab = 17^2 - 2×60 = 289 - 120 = 169$。
又因为 $c = 13$，所以 $c^2 = 13^2 = 169$。
因此，$a^2 + b^2 = c^2$，故 $\triangle ABC$ 是直角三角形。

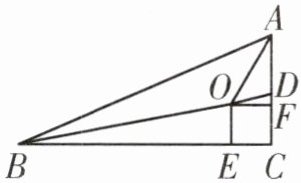
2. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,BD 是$Rt△ABC$的一条角平分线,点 O,E,F 分别在 BD,BC,AC 上,且四边形 OECF 是正方形.
(1)求证:点 O 在$∠BAC$的平分线上;
(2)若$AC= 5,BC= 12$,求 OE 的长.

答案：
(1)证明：连接OA，过点O作OM⊥AB于点M。
∵四边形OECF是正方形，
∴OE=OF，OE⊥BC，OF⊥AC，∠C=90°。
∵BD平分∠ABC，OM⊥AB，OE⊥BC，
∴OM=OE=OF。
∵OF⊥AC，OM⊥AB，
∴点O在∠BAC的平分线上。
(2)解：在Rt△ABC中，∠C=90°，AC=5，BC=12，
∴AB=$\sqrt{AC^2+BC^2}=\sqrt{5^2+12^2}=13$。
设OE=EC=CF=x，则BE=BC-EC=12-x，AF=AC-CF=5-x。
由
(1)知OM=OE=x，AM=AF=5-x，BM=BE=12-x。
∵AB=AM+BM，
∴13=(5-x)+(12-x)，
解得x=2。
∴OE=2。