2025年智趣暑假作业八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智趣暑假作业八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在$□ ABCD$中,下列结论一定正确的是(
A.$AC= BD$
B.$AC\perp BD$
C.$AB= CD$
D.$AB= BC$
C
)A.$AC= BD$
B.$AC\perp BD$
C.$AB= CD$
D.$AB= BC$
答案:
解:在平行四边形$ABCD$中,根据平行四边形的性质,对边相等,即$AB = CD$,$AD = BC$。
A选项,对角线相等是矩形的性质,平行四边形对角线不一定相等,故A错误;
B选项,对角线互相垂直是菱形的性质,平行四边形对角线不一定垂直,故B错误;
C选项,$AB = CD$符合平行四边形对边相等的性质,故C正确;
D选项,邻边相等是菱形的性质,平行四边形邻边不一定相等,故D错误。
答案:C
A选项,对角线相等是矩形的性质,平行四边形对角线不一定相等,故A错误;
B选项,对角线互相垂直是菱形的性质,平行四边形对角线不一定垂直,故B错误;
C选项,$AB = CD$符合平行四边形对边相等的性质,故C正确;
D选项,邻边相等是菱形的性质,平行四边形邻边不一定相等,故D错误。
答案:C
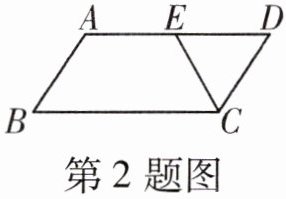
2. 如图,在平行四边形$ABCD$中,$AD= 2AB$,$CE平分\angle BCD交AD边于点E$,且$AE= 3$,则$AB$的长为(
A.4
B.3
C.$\frac{5}{2}$
D.2
B
) 
A.4
B.3
C.$\frac{5}{2}$
D.2
答案:
解:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD//BC,
∴∠DEC=∠BCE。
∵CE平分∠BCD,
∴∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DE=CD。
设AB=x,则CD=x,AD=2AB=2x。
∵AE=3,AD=AE+DE,
∴2x=3+x,
解得x=3,即AB=3。
答案:B
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD//BC,
∴∠DEC=∠BCE。
∵CE平分∠BCD,
∴∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DE=CD。
设AB=x,则CD=x,AD=2AB=2x。
∵AE=3,AD=AE+DE,
∴2x=3+x,
解得x=3,即AB=3。
答案:B
3. 已知$□ ABCD$中,$\angle A+\angle C= 200^{\circ}$,则$\angle B$的度数是(
A.$100^{\circ}$
B.$160^{\circ}$
C.$80^{\circ}$
D.$60^{\circ}$
C
)A.$100^{\circ}$
B.$160^{\circ}$
C.$80^{\circ}$
D.$60^{\circ}$
答案:
解:在平行四边形$ABCD$中,$\angle A = \angle C$,$\angle A + \angle B = 180^{\circ}$。
因为$\angle A + \angle C = 200^{\circ}$,所以$2\angle A = 200^{\circ}$,$\angle A = 100^{\circ}$。
则$\angle B = 180^{\circ} - \angle A = 180^{\circ} - 100^{\circ} = 80^{\circ}$。
答案:C
因为$\angle A + \angle C = 200^{\circ}$,所以$2\angle A = 200^{\circ}$,$\angle A = 100^{\circ}$。
则$\angle B = 180^{\circ} - \angle A = 180^{\circ} - 100^{\circ} = 80^{\circ}$。
答案:C
4. 如图,在平行四边形$ABCD$中,$AB= 3cm$,$BC= 5cm$,对角线$AC$,$BD相交于点O$,则$OA$的取值范围是(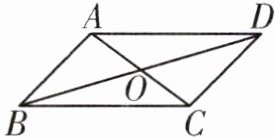
A.$2cm<OA<5cm$
B.$2cm<OA<8cm$
C.$1cm<OA<4cm$
D.$3cm<OA<8cm$
C
)
A.$2cm<OA<5cm$
B.$2cm<OA<8cm$
C.$1cm<OA<4cm$
D.$3cm<OA<8cm$
答案:
解:在平行四边形$ABCD$中,$OA = \frac{1}{2}AC$。
在$\triangle ABC$中,$AB = 3cm$,$BC = 5cm$,根据三角形三边关系:$BC - AB < AC < BC + AB$,即$5 - 3 < AC < 5 + 3$,$2cm < AC < 8cm$。
所以$1cm < \frac{1}{2}AC < 4cm$,即$1cm < OA < 4cm$。
答案:C
在$\triangle ABC$中,$AB = 3cm$,$BC = 5cm$,根据三角形三边关系:$BC - AB < AC < BC + AB$,即$5 - 3 < AC < 5 + 3$,$2cm < AC < 8cm$。
所以$1cm < \frac{1}{2}AC < 4cm$,即$1cm < OA < 4cm$。
答案:C
1. 在平面直角坐标系中,平行四边形$ABCD的顶点A$,$B$,$D的坐标分别是(0,0)$,$(5,0)$,$(2,3)$,则顶点$C$的坐标是
(7,3)
.
答案:
解:
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,AD=BC,AD//BC。
∵A(0,0),B(5,0),
∴AB的长度为5-0=5,AB在x轴上,方向向右。
∵D(2,3),
∴从D点向右平移5个单位长度得到C点。
∴C点的横坐标为2+5=7,纵坐标为3。
∴顶点C的坐标是(7,3)。
答案:(7,3)
∵四边形ABCD是平行四边形,
∴AB=CD,AB//CD,AD=BC,AD//BC。
∵A(0,0),B(5,0),
∴AB的长度为5-0=5,AB在x轴上,方向向右。
∵D(2,3),
∴从D点向右平移5个单位长度得到C点。
∴C点的横坐标为2+5=7,纵坐标为3。
∴顶点C的坐标是(7,3)。
答案:(7,3)
2. 在$□ ABCD$中,$AC= 6cm$,$BD= 8cm$,设$AB= a cm$,则$a$的取值范围是
$1 < a < 7$
.
答案:
解:在平行四边形$ABCD$中,对角线$AC$与$BD$互相平分,
所以$OA = \frac{1}{2}AC = \frac{1}{2}×6 = 3cm$,$OB = \frac{1}{2}BD = \frac{1}{2}×8 = 4cm$。
在$\triangle AOB$中,根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,
可得$OB - OA < AB < OA + OB$,即$4 - 3 < a < 3 + 4$,
所以$1 < a < 7$。
$1 < a < 7$
所以$OA = \frac{1}{2}AC = \frac{1}{2}×6 = 3cm$,$OB = \frac{1}{2}BD = \frac{1}{2}×8 = 4cm$。
在$\triangle AOB$中,根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,
可得$OB - OA < AB < OA + OB$,即$4 - 3 < a < 3 + 4$,
所以$1 < a < 7$。
$1 < a < 7$
查看更多完整答案,请扫码查看


