《2025年智趣暑假作业八年级数学人教版》

3. 如图所示,在 $Rt△ABC$ 中,$∠ACB = 90^{\circ}$,$D$,$E$ 分别是 $AB$,$BC$ 的中点,点 $F$ 在 $AC$ 的延长线上,$CF = \frac{1}{2}AC$,若 $CD$ 的长为 $10 cm$,则 $EF$ 的长为10$cm$.

答案： 解：
∵在$Rt△ABC$中，$∠ACB=90^{\circ}$，$D$是$AB$中点，
∴$CD=\frac{1}{2}AB=10\,\text{cm}$，则$AB=20\,\text{cm}$。
∵$D$，$E$分别是$AB$，$BC$中点，
∴$DE$是$△ABC$的中位线，
∴$DE// AC$，$DE=\frac{1}{2}AC$。
∵$CF=\frac{1}{2}AC$，
∴$DE=CF$，且$DE// CF$，
∴四边形$DCFE$是平行四边形，
∴$EF=CD=10\,\text{cm}$。
答案：$10$

1. 如图,$AB$,$CD$ 相交于点 $O$,$AC// DB$,$AO = BO$,$E$,$F$ 分别是 $OC$,$OD$ 的中点,求证：四边形 $AFBE$ 是平行四边形.

答案： 证明：$\because AC// DB$，
$\therefore \angle C=\angle D$。
又$\because \angle AOC=\angle BOD$，$AO=BO$，
$\therefore \triangle AOC\cong \triangle BOD$（AAS）。
$\therefore CO=DO$。
$\because E$，$F$分别是$OC$，$OD$的中点，
$\therefore OE=\frac{1}{2}OC$，$OF=\frac{1}{2}OD$，
$\therefore OE=OF$。
$\because AO=BO$，$EO=FO$，
$\therefore$ 四边形$AFBE$是平行四边形。

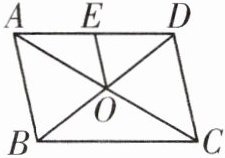
2. 如图,$□ ABCD$ 的对角线 $AC$,$BD$ 交于点 $O$,点 $E$ 是 $AD$ 的中点,$△BCD$ 的周长为 $18$,求 $△DEO$ 的周长.

答案： 解：
∵四边形ABCD是平行四边形，
∴O是BD中点，AD=BC，AB=CD，
∵E是AD中点，
∴EO是△ABD的中位线，
∴EO=$\frac{1}{2}$AB，DE=$\frac{1}{2}$AD=$\frac{1}{2}$BC，DO=$\frac{1}{2}$BD，
∵△BCD的周长为18，即BC+CD+BD=18，
∴△DEO的周长=DE+EO+DO=$\frac{1}{2}$BC+$\frac{1}{2}$AB+$\frac{1}{2}$BD，
又
∵AB=CD，
∴△DEO的周长=$\frac{1}{2}$(BC+CD+BD)=$\frac{1}{2}$×18=9．
答：△DEO的周长为9．