12. 将一副三角板拼成如图2-8所示的图形,过点$C作CF平分\angle DCE交DE于点F$。
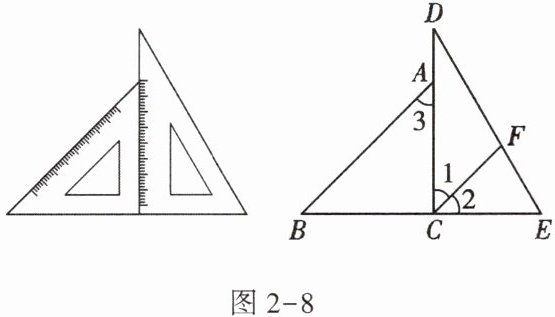
(1)试说明$CF// AB$;
解:因为 $ CF $ 平分 $ \angle DCE $,所以 $ \angle 1 = \angle 2 = \frac { 1 } { 2 } \angle DCE $。
因为 $ \angle DCE = 90 ^ { \circ } $,所以 $ \angle 1 = 45 ^ { \circ } $。
因为 $ \angle 3 = 45 ^ { \circ } $,所以 $ \angle 1 = \angle 3 $。
所以 $ CF // AB $(内错角相等,两直线平行)。
(2)求$\angle DFC$的度数。
解:因为 $ \angle D = 30 ^ { \circ } $,$ \angle 1 = 45 ^ { \circ } $,所以 $ \angle DFC = 180 ^ { \circ } - 30 ^ { \circ } - 45 ^ { \circ } =

(1)试说明$CF// AB$;
解:因为 $ CF $ 平分 $ \angle DCE $,所以 $ \angle 1 = \angle 2 = \frac { 1 } { 2 } \angle DCE $。
因为 $ \angle DCE = 90 ^ { \circ } $,所以 $ \angle 1 = 45 ^ { \circ } $。
因为 $ \angle 3 = 45 ^ { \circ } $,所以 $ \angle 1 = \angle 3 $。
所以 $ CF // AB $(内错角相等,两直线平行)。
(2)求$\angle DFC$的度数。
解:因为 $ \angle D = 30 ^ { \circ } $,$ \angle 1 = 45 ^ { \circ } $,所以 $ \angle DFC = 180 ^ { \circ } - 30 ^ { \circ } - 45 ^ { \circ } =
105°
$。
答案:
(1) 因为 $ CF $ 平分 $ \angle DCE $,所以 $ \angle 1 = \angle 2 = \frac { 1 } { 2 } \angle DCE $。
因为 $ \angle DCE = 90 ^ { \circ } $,所以 $ \angle 1 = 45 ^ { \circ } $。
因为 $ \angle 3 = 45 ^ { \circ } $,所以 $ \angle 1 = \angle 3 $。
所以 $ CF // AB $(内错角相等,两直线平行)。
(2) 因为 $ \angle D = 30 ^ { \circ } $,$ \angle 1 = 45 ^ { \circ } $,所以 $ \angle DFC = 180 ^ { \circ } - 30 ^ { \circ } - 45 ^ { \circ } = 105 ^ { \circ } $。
(1) 因为 $ CF $ 平分 $ \angle DCE $,所以 $ \angle 1 = \angle 2 = \frac { 1 } { 2 } \angle DCE $。
因为 $ \angle DCE = 90 ^ { \circ } $,所以 $ \angle 1 = 45 ^ { \circ } $。
因为 $ \angle 3 = 45 ^ { \circ } $,所以 $ \angle 1 = \angle 3 $。
所以 $ CF // AB $(内错角相等,两直线平行)。
(2) 因为 $ \angle D = 30 ^ { \circ } $,$ \angle 1 = 45 ^ { \circ } $,所以 $ \angle DFC = 180 ^ { \circ } - 30 ^ { \circ } - 45 ^ { \circ } = 105 ^ { \circ } $。
13. 如图2-9,$AB// CD$,$EF\perp AB于点O$,$\angle 2 = 135^{\circ}$,求$\angle 1$的度数。
下面提供三个思路:①过点$F作FH// AB$;②延长$EF交CD于点I$;③延长$GF交AB于点K$。请你利用三个思路中的任意一个,求$\angle 1$的度数。
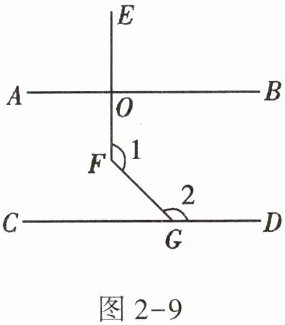
$\angle 1=$
例如:延长 $ GF $ 交 $ AB $ 于点 $ K $。
因为 $ AB // CD $,所以 $ \angle 2 + \angle BKG = 180 ^ { \circ } $。
因为 $ \angle 2 = 135 ^ { \circ } $,所以 $ \angle BKG = 45 ^ { \circ } $。
又因为 $ EF \perp AB $ 于点 $ O $,所以 $ \angle AOF = 90 ^ { \circ } $。
所以 $ \angle KFO = 45 ^ { \circ } $。
所以 $ \angle 1 = 135 ^ { \circ } $。
下面提供三个思路:①过点$F作FH// AB$;②延长$EF交CD于点I$;③延长$GF交AB于点K$。请你利用三个思路中的任意一个,求$\angle 1$的度数。

$\angle 1=$
$135^{\circ}$
。例如:延长 $ GF $ 交 $ AB $ 于点 $ K $。
因为 $ AB // CD $,所以 $ \angle 2 + \angle BKG = 180 ^ { \circ } $。
因为 $ \angle 2 = 135 ^ { \circ } $,所以 $ \angle BKG = 45 ^ { \circ } $。
又因为 $ EF \perp AB $ 于点 $ O $,所以 $ \angle AOF = 90 ^ { \circ } $。
所以 $ \angle KFO = 45 ^ { \circ } $。
所以 $ \angle 1 = 135 ^ { \circ } $。
答案:
$ \angle 1 = 135 ^ { \circ } $。
例如:延长 $ GF $ 交 $ AB $ 于点 $ K $。
因为 $ AB // CD $,所以 $ \angle 2 + \angle BKG = 180 ^ { \circ } $。
因为 $ \angle 2 = 135 ^ { \circ } $,所以 $ \angle BKG = 45 ^ { \circ } $。
又因为 $ EF \perp AB $ 于点 $ O $,所以 $ \angle AOF = 90 ^ { \circ } $。
所以 $ \angle KFO = 45 ^ { \circ } $。
所以 $ \angle 1 = 135 ^ { \circ } $。
例如:延长 $ GF $ 交 $ AB $ 于点 $ K $。
因为 $ AB // CD $,所以 $ \angle 2 + \angle BKG = 180 ^ { \circ } $。
因为 $ \angle 2 = 135 ^ { \circ } $,所以 $ \angle BKG = 45 ^ { \circ } $。
又因为 $ EF \perp AB $ 于点 $ O $,所以 $ \angle AOF = 90 ^ { \circ } $。
所以 $ \angle KFO = 45 ^ { \circ } $。
所以 $ \angle 1 = 135 ^ { \circ } $。
查看更多完整答案,请扫码查看


