16. 先化简,再求值:$(3x + 2)(3x - 2) - 5x(x - 1) - (2x - 1)^{2}$,其中$x = -\frac{1}{3}$。
答案:
原式 $= 9x^{2} - 4 - (5x^{2} - 5x) - (4x^{2} - 4x + 1) = 9x^{2} - 4 - 5x^{2} + 5x - 4x^{2} + 4x - 1 = 9x - 5$。
当 $x = - \frac{1}{3}$ 时,原式 $= 9\times(-\frac{1}{3}) - 5 = - 3 - 5 = - 8$。
当 $x = - \frac{1}{3}$ 时,原式 $= 9\times(-\frac{1}{3}) - 5 = - 3 - 5 = - 8$。
17. 对于任何有理数,我们规定$\begin{vmatrix}a&b\\c&d\end{vmatrix}的意义是\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc$。
(1)按照这个规定,请你计算$\begin{vmatrix}5&6\\7&8\end{vmatrix}$的值。
(2)按照这个规定,请你计算:当$x^{2} - 3x + 1 = 0$时,$\begin{vmatrix}x + 1&3x\\x - 2&x - 1\end{vmatrix}$的值。
(1)按照这个规定,请你计算$\begin{vmatrix}5&6\\7&8\end{vmatrix}$的值。
-2
(2)按照这个规定,请你计算:当$x^{2} - 3x + 1 = 0$时,$\begin{vmatrix}x + 1&3x\\x - 2&x - 1\end{vmatrix}$的值。
1
答案:
(1) $ \begin{vmatrix} 5 & 6 \\ 7 & 8 \end{vmatrix} = 5\times8 - 6\times7 = - 2$。
(2) $ \begin{vmatrix} x + 1 & 3x \\ x - 2 & x - 1 \end{vmatrix} = (x + 1)(x - 1) - 3x(x - 2) = x^{2} - 1 - 3x^{2} + 6x = - 2x^{2} + 6x - 1$。
又因为 $x^{2} - 3x + 1 = 0$,所以 $x^{2} - 3x = - 1$。
所以原式 $= - 2(x^{2} - 3x) - 1 = - 2\times(- 1) - 1 = 1$。
(1) $ \begin{vmatrix} 5 & 6 \\ 7 & 8 \end{vmatrix} = 5\times8 - 6\times7 = - 2$。
(2) $ \begin{vmatrix} x + 1 & 3x \\ x - 2 & x - 1 \end{vmatrix} = (x + 1)(x - 1) - 3x(x - 2) = x^{2} - 1 - 3x^{2} + 6x = - 2x^{2} + 6x - 1$。
又因为 $x^{2} - 3x + 1 = 0$,所以 $x^{2} - 3x = - 1$。
所以原式 $= - 2(x^{2} - 3x) - 1 = - 2\times(- 1) - 1 = 1$。
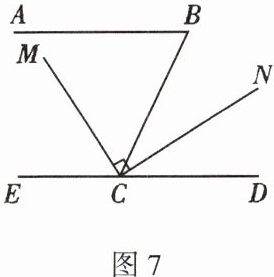
18. 如图7,已知$AB// CD$,$∠B = 65^{\circ}$,$CM平分∠BCE$,$∠MCN = 90^{\circ}$,求$∠DCN$的度数。
解:因为 $AB // CD$,所以 $ \angle B + \angle BCE = 180^{\circ}$(两直线平行,同旁内角互补)。
因为 $ \angle B = 65^{\circ}$,所以 $ \angle BCE = $
因为 $CM$ 平分 $ \angle BCE$,所以 $ \angle ECM = \frac{1}{2} \angle BCE = $
因为 $ \angle ECM + \angle MCN + \angle DCN = 180^{\circ}$,$ \angle MCN = 90^{\circ}$,
所以 $ \angle DCN = 180^{\circ} - \angle ECM - \angle MCN = 180^{\circ} - 57.5^{\circ} - 90^{\circ} = $

解:因为 $AB // CD$,所以 $ \angle B + \angle BCE = 180^{\circ}$(两直线平行,同旁内角互补)。
因为 $ \angle B = 65^{\circ}$,所以 $ \angle BCE = $
115°
。因为 $CM$ 平分 $ \angle BCE$,所以 $ \angle ECM = \frac{1}{2} \angle BCE = $
57.5°
。因为 $ \angle ECM + \angle MCN + \angle DCN = 180^{\circ}$,$ \angle MCN = 90^{\circ}$,
所以 $ \angle DCN = 180^{\circ} - \angle ECM - \angle MCN = 180^{\circ} - 57.5^{\circ} - 90^{\circ} = $
32.5°
。
答案:
因为 $AB // CD$,所以 $ \angle B + \angle BCE = 180^{\circ}$(两直线平行,同旁内角互补)。
因为 $ \angle B = 65^{\circ}$,所以 $ \angle BCE = 115^{\circ}$。
因为 $CM$ 平分 $ \angle BCE$,所以 $ \angle ECM = \frac{1}{2} \angle BCE = 57.5^{\circ}$。
因为 $ \angle ECM + \angle MCN + \angle DCN = 180^{\circ}$,$ \angle MCN = 90^{\circ}$,
所以 $ \angle DCN = 180^{\circ} - \angle ECM - \angle MCN = 180^{\circ} - 57.5^{\circ} - 90^{\circ} = 32.5^{\circ}$。
因为 $ \angle B = 65^{\circ}$,所以 $ \angle BCE = 115^{\circ}$。
因为 $CM$ 平分 $ \angle BCE$,所以 $ \angle ECM = \frac{1}{2} \angle BCE = 57.5^{\circ}$。
因为 $ \angle ECM + \angle MCN + \angle DCN = 180^{\circ}$,$ \angle MCN = 90^{\circ}$,
所以 $ \angle DCN = 180^{\circ} - \angle ECM - \angle MCN = 180^{\circ} - 57.5^{\circ} - 90^{\circ} = 32.5^{\circ}$。
19. 一次越野赛跑中,当李明跑了$1600m$时,小刚跑了$1450m$,此后两人匀速跑的路程$s与时间t$的关系如图8,结合图象解答下列问题:
(1)请你根据图象写出两条信息;
①
②
(2)求图中$s_{1}和s_{0}$的值。
$s_{1}=$
(1)请你根据图象写出两条信息;
①
小刚比李明早到终点100s
;②
两人匀速跑时,小刚的速度大于李明的速度
。(2)求图中$s_{1}和s_{0}$的值。
$s_{1}=$
2050
,$s_{0}=$1750
。
答案:
(1) 由图象可得出:
① 小刚比李明早到终点 $100s$;
② 两人匀速跑时,小刚的速度大于李明的速度。
(2) 因为 $ \frac{s_1 - 1450}{200} \times 100 - \frac{s_1 - 1600}{300} \times 100 = 150$,所以 $s_1 = 2050$。
所以 $s_0 = 1450 + \frac{s_1 - 1450}{200} \times 100 = 1750$。
(1) 由图象可得出:
① 小刚比李明早到终点 $100s$;
② 两人匀速跑时,小刚的速度大于李明的速度。
(2) 因为 $ \frac{s_1 - 1450}{200} \times 100 - \frac{s_1 - 1600}{300} \times 100 = 150$,所以 $s_1 = 2050$。
所以 $s_0 = 1450 + \frac{s_1 - 1450}{200} \times 100 = 1750$。
查看更多完整答案,请扫码查看


