相交线与平行线
基本概念与性质
余角的概念:①
补角的概念:②
对顶角的概念及性质:③
余角的性质:④
补角的性质:⑤
同一平面内,过一点有且只有一条直线与已知直线垂直
直线外一点与直线上各点连接的所有线段中,⑥最短
两直线平行的条件
同位角⑦,两直线平行
过直线外一点⑧直线与这条直线平行
平行于同一条直线的两条直线⑨
⑩相等,两直线平行
同旁内角互补,⑪
两直线平行的特征
两直线平行,同位角⑫
两直线平行,⑬相等
两直线平行,⑭
基本概念与性质
余角的概念:①
补角的概念:②
对顶角的概念及性质:③
余角的性质:④
补角的性质:⑤
同一平面内,过一点有且只有一条直线与已知直线垂直
直线外一点与直线上各点连接的所有线段中,⑥最短
两直线平行的条件
同位角⑦,两直线平行
过直线外一点⑧直线与这条直线平行
平行于同一条直线的两条直线⑨
⑩相等,两直线平行
同旁内角互补,⑪
两直线平行的特征
两直线平行,同位角⑫
两直线平行,⑬相等
两直线平行,⑭
答案:
①如果两个角的和等于$90^{\circ}$(直角),就说这两个角互为余角;
②如果两个角的和等于$180^{\circ}$(平角),就说这两个角互为补角;
③有公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,对顶角相等;
④同角(或等角)的余角相等;
⑤同角(或等角)的补角相等;
⑥垂线段;
⑦相等;
⑧有且只有一条;
⑨平行;
⑩内错角;
⑪两直线平行;
⑫相等;
⑬内错角;
⑭同旁内角互补。
②如果两个角的和等于$180^{\circ}$(平角),就说这两个角互为补角;
③有公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,对顶角相等;
④同角(或等角)的余角相等;
⑤同角(或等角)的补角相等;
⑥垂线段;
⑦相等;
⑧有且只有一条;
⑨平行;
⑩内错角;
⑪两直线平行;
⑫相等;
⑬内错角;
⑭同旁内角互补。
1. 下列说法正确的是(
A. 有公共顶点的角是对顶角
B. 相等的角是对顶角
C. 对顶角相等
D. 不是对顶角的角不相等
C
)A. 有公共顶点的角是对顶角
B. 相等的角是对顶角
C. 对顶角相等
D. 不是对顶角的角不相等
答案:
C
2. 一个角的补角是它的余角的3倍,则这个角的度数是(
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $75^{\circ}$
B
)A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $75^{\circ}$
答案:
B
3. 如图2-1,$AB// CD$,$\angle B = 75^{\circ}$,$\angle E = 27^{\circ}$,则$\angle D$的度数为(
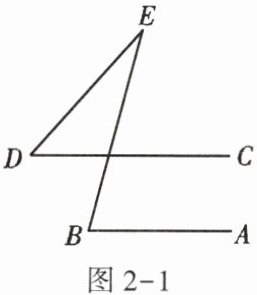
A. $45^{\circ}$
B. $48^{\circ}$
C. $50^{\circ}$
D. $58^{\circ}$
B
)
A. $45^{\circ}$
B. $48^{\circ}$
C. $50^{\circ}$
D. $58^{\circ}$
答案:
B
查看更多完整答案,请扫码查看


