《2025年暑假作业本大象出版社七年级数学、生物学合订本》

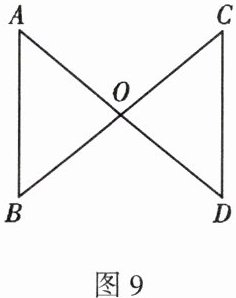
20. 如图9,$AD$,$BC相交于点O$,$AB = CD$。请你添加一个条件使得$△AOB≌△COD$,并说明你的理由。

添加的条件是$\angle A = \angle C$。理由如下：在$\triangle AOB$和$\triangle COD$中，$\angle A = \angle C$，$\angle AOB = \angle COD$，$AB = CD$，所以$\triangle AOB \cong \triangle COD (AAS)$。

答案： 答案不唯一，如添加条件：$ \angle A = \angle C$。理由如下：
在 $ \triangle AOB$ 和 $ \triangle COD$ 中，$ \angle A = \angle C$，$ \angle AOB = \angle COD$，$AB = CD$，所以 $ \triangle AOB \cong \triangle COD (AAS)$。

21. 一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球。红球的个数是黑球个数的2倍多40,从袋中任取一个球是白球的概率是$\frac{1}{29}$。
(1)求袋中红球的个数；
(2)求从袋中任取一个球是黑球的概率。

答案：
(1) 因为从袋中任取一个球是白球的概率是 $ \frac{1}{29}$，所以袋中白球的个数为 $290 \times \frac{1}{29} = 10$。
设袋中黑球的个数为 $x$，则袋中红球的个数为 $2x + 40$。
根据题意，得 $(2x + 40) + x + 10 = 290$。解得 $x = 80$。
所以 $2x + 40 = 200$。所以袋中红球的个数为 $200$。
(2) 从袋中任取一个球是黑球的概率为 $ \frac{80}{290} = \frac{8}{29}$。

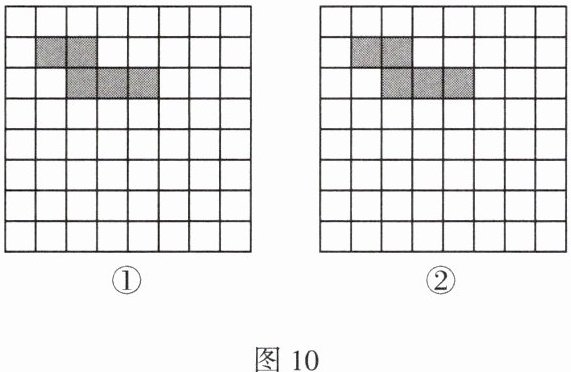
22. 李明同学准备制作一个正方体形盒子,他先用5个大小一样的正方形制成如图10所示的拼接图形(阴影部分),折叠后发现少一个面,请你在图中的拼接图形上再接一个正方形,使新拼成的图形经过折叠后能成为一个封闭的正方体形盒子。(添加的正方形用阴影表示,在图10①、图10②中各画一个符合要求的图形即可)

答案：
答案不唯一，如下图所示。
　

23. 如图11,在$△ABC$中,$D是BC$边上的一点,$AB = DB$,$BE平分∠ABC$,交$AC边于点E$,连接$DE$。

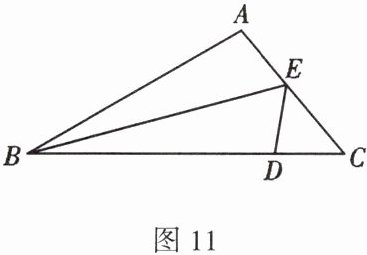
(1)试说明$△ABE≌△DBE$；
因为 $BE$ 平分 $ \angle ABC$，所以 $ \angle ABE = \angle DBE$。在 $ \triangle ABE$ 和 $ \triangle DBE$ 中，$AB = DB$，$ \angle ABE = \angle DBE$，$BE = BE$，所以 $ \triangle ABE \cong \triangle DBE (SAS)$。
(2)若$∠A = 100^{\circ}$,$∠C = 50^{\circ}$,求$∠AEB$的度数。
因为 $ \angle A = 100^{\circ}$，$ \angle C = 50^{\circ}$，所以 $ \angle ABC = 30^{\circ}$。因为 $BE$ 平分 $ \angle ABC$，所以 $ \angle ABE = \angle DBE = \frac{1}{2} \angle ABC = 15^{\circ}$。在 $ \triangle ABE$ 中，$ \angle AEB = 180^{\circ} - \angle A - \angle ABE = 180^{\circ} - 100^{\circ} - 15^{\circ} = 65^{\circ}$。

答案：
(1) 因为 $BE$ 平分 $ \angle ABC$，所以 $ \angle ABE = \angle DBE$。在 $ \triangle ABE$ 和 $ \triangle DBE$ 中，$AB = DB$，$ \angle ABE = \angle DBE$，$BE = BE$，所以 $ \triangle ABE \cong \triangle DBE (SAS)$。
(2) 因为 $ \angle A = 100^{\circ}$，$ \angle C = 50^{\circ}$，所以 $ \angle ABC = 30^{\circ}$。因为 $BE$ 平分 $ \angle ABC$，所以 $ \angle ABE = \angle DBE = \frac{1}{2} \angle ABC = 15^{\circ}$。在 $ \triangle ABE$ 中，$ \angle AEB = 180^{\circ} - \angle A - \angle ABE = 180^{\circ} - 100^{\circ} - 15^{\circ} = 65^{\circ}$。