4.在10张卡片中,有6张上面写着偶数,4张上面写着奇数,从中任取5张卡片的必然事件是(
A.其中必有一张是奇数卡片
B.其中至少有一张是奇数卡片
C.其中至少有一张是偶数卡片
D.其中至少有两张是偶数卡片
C
)A.其中必有一张是奇数卡片
B.其中至少有一张是奇数卡片
C.其中至少有一张是偶数卡片
D.其中至少有两张是偶数卡片
答案:
C
5.图3-2所示的是一个游戏转盘,自由转动转盘,当转盘停止后,若指针落在所示区域内事件发生的概率依次记为r,s,t,k,则(
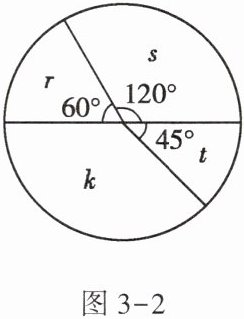
A.$s + t<\frac{1}{2}$
B.$s = 3t$
C.$k<r + t$
D.$k + r<s + t$
A
)
A.$s + t<\frac{1}{2}$
B.$s = 3t$
C.$k<r + t$
D.$k + r<s + t$
答案:
A
6.两位同学进行计算比赛,甲同学共做了30道题,错了5题;乙同学共做了35道题,错了7题。则______
甲
(填“甲”或“乙”)同学的正确率高。
答案:
甲
7.在“践行生态文明,你我一起行动”主题有奖竞赛活动中,某班共设置“生态知识”“生态技能”“生态习惯”“生态文明”四个类别的竞赛内容,如果参赛同学抽到每一类别的可能性相同,那么小宇参赛时抽到“生态知识”的概率是
0.25
。
答案:
0.25
8.小明把如图3-3所示的正方形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是______
0.25
。
答案:
0.25
9.口袋中放有黄、白、红三种颜色的小球各1个,这3个球除颜色外没有任何区别,随机从口袋中任取1个球,写出一个可能发生的事件:
取出的可能是黄球
。
答案:
答案不唯一,如取出的可能是黄(或白或红)球
10.两名同学进行射击比赛,甲同学射击20次,击中15次;乙同学射击15次,击中9次。则两人的命中率分别是$P$(甲击中)=
0.75
,$P$(乙击中)=0.6
。
答案:
0.75 0.6
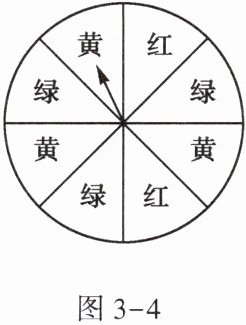
11.图3-4所示的是一个转盘。转盘被分成8个相同的图形,颜色分为红、绿、黄三种。指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个图形的交线时,当作指向右边的图形)。求下列事件的概率:
(1)指针指向红色;
(2)指针指向黄色或绿色。
(1)指针指向红色;
$\frac{1}{4}$
(2)指针指向黄色或绿色。
$\frac{3}{4}$

答案:
按颜色把 8 个扇形分为红 1、红 2、绿 1、绿 2、绿 3、黄 1、黄 2、黄 3,所有可能结果的总数为 8。
(1) 指针指向红色的结果有 2 个,所以 $ P(\text{指针指向红色}) = \frac{2}{8} = \frac{1}{4} $。
(2) 指针指向黄色或绿色的结果有 $ 3 + 3 = 6 $ (个),所以 $ P(\text{指针指向黄色或绿色}) = \frac{6}{8} = \frac{3}{4} $。
(1) 指针指向红色的结果有 2 个,所以 $ P(\text{指针指向红色}) = \frac{2}{8} = \frac{1}{4} $。
(2) 指针指向黄色或绿色的结果有 $ 3 + 3 = 6 $ (个),所以 $ P(\text{指针指向黄色或绿色}) = \frac{6}{8} = \frac{3}{4} $。
查看更多完整答案,请扫码查看


