8. 如图5,在由6个大小相同的边长为1的小正方形组成的方格中,A,B,C是三个格点(即小正方形的顶点),判断AB与BC的数量关系和位置关系,并说明理由。
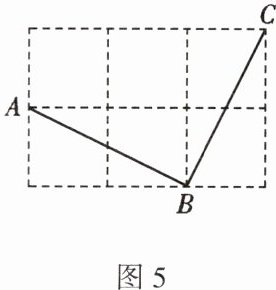

连接AC,由勾股定理,得AB²=1²+2²=5,BC²=1²+2²=5,AC²=1²+3²=10,所以AB=BC,AB²+BC²=AC²。所以△ABC是直角三角形,且∠ABC=90°。所以AB⊥BC,即AB=BC,AB⊥BC。
答案:
连接$AC$,由勾股定理,得$AB^{2} = 1^{2} + 2^{2} = 5$,$BC^{2} = 1^{2} + 2^{2} = 5$,$AC^{2} = 1^{2} + 3^{2} = 10$,所以$AB = BC$,$AB^{2} + BC^{2} = AC^{2}$。
所以$\triangle ABC$是直角三角形,且$\angle ABC = 90^{\circ}$。
所以$AB \perp BC$,即$AB = BC$,$AB \perp BC$。
所以$\triangle ABC$是直角三角形,且$\angle ABC = 90^{\circ}$。
所以$AB \perp BC$,即$AB = BC$,$AB \perp BC$。
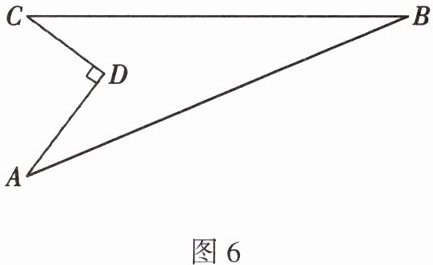
9. 如图6,某住宅小区在施工过程中留下了一块空地,已知$ AD = 4 m $,$ CD = 3 m $,$ ∠ADC = 90° $,$ AB = 13 m $,$ BC = 12 m $,求这块空地的面积。

24
答案:
连接$AC$。在$\triangle ACD$中,因为$AD = 4\text{ m}$,$CD = 3\text{ m}$,$\angle ADC = 90^{\circ}$,所以$AC = 5\text{ m}$。
又因为$AC^{2} + BC^{2} = 5^{2} + 12^{2} = 13^{2} = AB^{2}$,
所以$\triangle ABC$是直角三角形。
所以这块空地的面积为$S_{\triangle ABC} - S_{\triangle ACD} = \frac{1}{2} \times 5 \times 12 - \frac{1}{2} \times 3 \times 4 = 24(\text{m}^{2})$。
又因为$AC^{2} + BC^{2} = 5^{2} + 12^{2} = 13^{2} = AB^{2}$,
所以$\triangle ABC$是直角三角形。
所以这块空地的面积为$S_{\triangle ABC} - S_{\triangle ACD} = \frac{1}{2} \times 5 \times 12 - \frac{1}{2} \times 3 \times 4 = 24(\text{m}^{2})$。
1. 小明从家中出发,先向正东方向前进了200m,接着又朝正南方向前进了150m,则这时小明离家的直线距离为(
A. 250m
B. 210m
C. 180m
D. 160m
A
)A. 250m
B. 210m
C. 180m
D. 160m
答案:
A
查看更多完整答案,请扫码查看


