《2025年名师测控九年级数学上册人教版》

25.(12 分)如图,在 $\triangle ABC$ 中,$\angle B = 90^{\circ},AB = 11\mathrm{cm},BC = 8\mathrm{cm}$,点 $P$ 从点 $A$ 出发,以每秒 1 cm 的速度沿 $AB$ 向点 $B$ 匀速运动,同时点 $Q$ 从点 $B$ 出发,以每秒 2 cm 的速度沿 $BC$ 向点 $C$ 匀速运动,到达点 $C$ 后返回点 $B$,当有一点停止运动时,另一点也停止运动,设运动时间为 $t\mathrm{s}$.

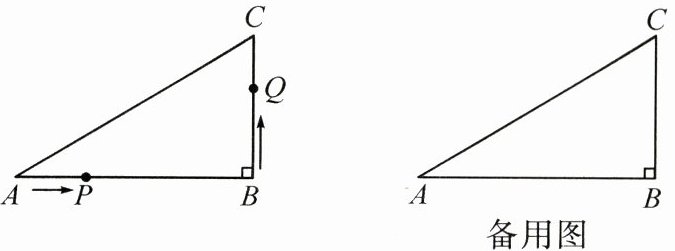
(1)当 $t = 1$ 时,$P,Q$ 两点间的距离为______$2\sqrt{26}\,\text{cm}$；
(2)是否存在 $t$,使得 $\triangle BPQ$ 是等腰三角形？若存在,请求出 $t$ 的值；若不存在,请说明理由；
存在，$t=\frac{11}{3}$或$5$
(3)是否存在 $t$,使得 $\triangle BPQ$ 的面积等于 $10\mathrm{cm}^{2}$？若存在,请求出 $t$ 的值；若不存在,请说明理由.
存在，$t = 1$或$6$

答案：
(1) 当$t = 1$时，$AP = 1×1 = 1\,\text{cm}$，则$BP = AB - AP = 11 - 1 = 10\,\text{cm}$，$BQ = 2×1 = 2\,\text{cm}$。在$\text{Rt}\triangle BPQ$中，由勾股定理得$PQ=\sqrt{BP^{2}+BQ^{2}}=\sqrt{10^{2}+2^{2}}=\sqrt{104}=2\sqrt{26}\,\text{cm}$。
(2) 存在。$\because\angle B = 90^{\circ}$，$\triangle BPQ$是等腰三角形时，$BP = BQ$。由题意：$BP=(11 - t)\,\text{cm}$。点$Q$运动全程时间为$\frac{2×8}{2}=8\,\text{s}$，点$P$运动时间为$11\,\text{s}$，故$t$取值范围为$0\leq t\leq8$。
- 当$0\leq t\leq4$时，$BQ = 2t\,\text{cm}$，则$11 - t = 2t$，解得$t=\frac{11}{3}$；
- 当$4\lt t\leq8$时，$BQ=(16 - 2t)\,\text{cm}$，则$11 - t = 16 - 2t$，解得$t = 5$。
综上，$t=\frac{11}{3}$或$5$。
(3) 存在。
- 当$0\leq t\leq4$时，$S_{\triangle BPQ}=\frac{1}{2}(11 - t)\cdot2t = 10$，即$t^{2}-11t + 10 = 0$，解得$t = 1$（$t = 10$舍去）；
- 当$4\lt t\leq8$时，$S_{\triangle BPQ}=\frac{1}{2}(11 - t)(16 - 2t)=10$，即$t^{2}-19t + 78 = 0$，解得$t = 6$（$t = 13$舍去）。
综上，$t = 1$或$6$。
答案：
(1)$2\sqrt{26}\,\text{cm}$；
(2)$t=\frac{11}{3}$或$5$；
(3)$t = 1$或$6$。