8. 如图,在$ \mathrm { Rt } \triangle A B C $中,$ \angle A C B = 90 ^ { \circ } $,$ \angle A = 30 ^ { \circ } $,$ B C = 2 $. 将$ \triangle A B C $绕点C按顺时针方向旋转$ n ^ { \circ } $后,得到$ \triangle E D C $,此时,点D在AB边上,斜边DE交AC边于点F,则n的值和图中阴影部分的面积分别为(
A.30,2
B.60,2
C.$ 60, \frac { \sqrt { 3 } } { 2 } $
D.$ 60, \sqrt { 3 } $
C
)A.30,2
B.60,2
C.$ 60, \frac { \sqrt { 3 } } { 2 } $
D.$ 60, \sqrt { 3 } $
答案:
C
9. 如图,在$ \mathrm { Rt } \triangle O A B $中,$ \angle O A B = 90 ^ { \circ } $,点B的坐标是$ ( - 2 \sqrt { 3 }, 2 ) $. 将$ \triangle O A B $绕点O顺时针旋转$ 60 ^ { \circ } $,得到$ \triangle O A _ { 1 } B _ { 1 } $,则点A的对应点$ A _ { 1 } $的坐标是(
A.$ ( 2 \sqrt { 3 }, 2 ) $
B.$ ( - \sqrt { 3 }, 3 ) $
C.$ ( \sqrt { 3 }, 3 ) $
D.$ ( 2 \sqrt { 3 }, - 2 ) $
B
)A.$ ( 2 \sqrt { 3 }, 2 ) $
B.$ ( - \sqrt { 3 }, 3 ) $
C.$ ( \sqrt { 3 }, 3 ) $
D.$ ( 2 \sqrt { 3 }, - 2 ) $
答案:
B
10. 如图,点E在正方形ABCD的边CD上,将$ \triangle A D E $绕点A顺时针旋转$ 90 ^ { \circ } 到 \triangle A B F $的位置,连接EF,过点A作EF的垂线,垂足为点H,与BC交于点G. 若$ B G = 3 $,$ C G = 2 $,则CE的长为(
A.$ \frac { 5 } { 4 } $
B.$ \frac { 15 } { 4 } $
C.4
D.$ \frac { 9 } { 2 } $
B
)A.$ \frac { 5 } { 4 } $
B.$ \frac { 15 } { 4 } $
C.4
D.$ \frac { 9 } { 2 } $
答案:
B
11. 如图,D是$ \triangle A B C $的边BC的中点,连接AD并延长到点E,使$ D E = A D $,连接BE.
(1)$ \triangle A D C $和
(2)已知$ \triangle A D C $的面积为4,则$ \triangle A B E $的面积是
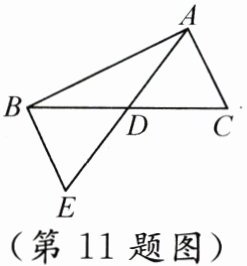
(1)$ \triangle A D C $和
$\triangle EDB$
成中心对称;(2)已知$ \triangle A D C $的面积为4,则$ \triangle A B E $的面积是
8
.
答案:
(1) $\triangle EDB$
(2) 8
(1) $\triangle EDB$
(2) 8
12. 如图,点A,B,C,D,O都在方格纸的格点上,若$ \triangle C O D 是由 \triangle A O B $绕点O按顺时针方向旋转而得到的,则旋转的角度为
90°
.
答案:
解:连接OA、OC。
由图可知,OA在第二象限与y轴正方向夹角约45°的格线上,OC在第一象限与x轴正方向夹角约45°的格线上。
OA绕点O顺时针旋转后与OC重合,通过格点距离判断,OA与OC垂直。
所以旋转角度为90°。
答案:90°
由图可知,OA在第二象限与y轴正方向夹角约45°的格线上,OC在第一象限与x轴正方向夹角约45°的格线上。
OA绕点O顺时针旋转后与OC重合,通过格点距离判断,OA与OC垂直。
所以旋转角度为90°。
答案:90°
13. 在平面直角坐标系中,点A的坐标为$ ( a, 3 ) $,点B的坐标为$ ( 4, b ) $. 若点A与点B关于原点O对称,则ab的值为____
12
.
答案:
解:
∵点A与点B关于原点O对称,
∴点A与点B的横、纵坐标均互为相反数。
∵点A的坐标为$(a, 3)$,点B的坐标为$(4, b)$,
∴$a = -4$,$b = -3$。
∴$ab = (-4)×(-3) = 12$。
12
∵点A与点B关于原点O对称,
∴点A与点B的横、纵坐标均互为相反数。
∵点A的坐标为$(a, 3)$,点B的坐标为$(4, b)$,
∴$a = -4$,$b = -3$。
∴$ab = (-4)×(-3) = 12$。
12
14. 如图,将一张直角三角形纸片ABC沿中位线DE剪开后,在平面上将$ \triangle B D E $绕着CB的中点D逆时针旋转$ 180 ^ { \circ } $,点E到了点$ E ^ { \prime } $位置,则四边形$ A C E ^ { \prime } E $的形状是
平行四边形
.
答案:
解:
∵DE是△ABC的中位线,
∴DE//AC,DE=$\frac{1}{2}$AC。
∵将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E'位置,
∴DE=DE',∠EDB=∠E'DB。
∵D是CB的中点,
∴CD=BD。
在△EDB和△E'DC中,
$\left\{\begin{array}{l} DE=DE' \\ ∠EDB=∠E'DC \\ BD=CD\end{array}\right.$,
∴△EDB≌△E'DC(SAS),
∴BE=CE',∠B=∠E'CD。
∵∠B+∠ACB=90°,∠E'CD+∠ACE'=180°-∠ACB,
∴∠ACE'=90°+∠ACB,
又
∵∠AEC'=∠AED+∠DEC',∠AED=∠ACB,∠DEC'=∠B,
∴∠AEC'=∠ACB+∠B=90°,
∴AE//CE'。
∵DE=DE',DE=$\frac{1}{2}$AC,
∴EE'=AC。
∵AE//CE',EE'=AC,
∴四边形ACE'E是平行四边形。
故答案为:平行四边形。
∵DE是△ABC的中位线,
∴DE//AC,DE=$\frac{1}{2}$AC。
∵将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E'位置,
∴DE=DE',∠EDB=∠E'DB。
∵D是CB的中点,
∴CD=BD。
在△EDB和△E'DC中,
$\left\{\begin{array}{l} DE=DE' \\ ∠EDB=∠E'DC \\ BD=CD\end{array}\right.$,
∴△EDB≌△E'DC(SAS),
∴BE=CE',∠B=∠E'CD。
∵∠B+∠ACB=90°,∠E'CD+∠ACE'=180°-∠ACB,
∴∠ACE'=90°+∠ACB,
又
∵∠AEC'=∠AED+∠DEC',∠AED=∠ACB,∠DEC'=∠B,
∴∠AEC'=∠ACB+∠B=90°,
∴AE//CE'。
∵DE=DE',DE=$\frac{1}{2}$AC,
∴EE'=AC。
∵AE//CE',EE'=AC,
∴四边形ACE'E是平行四边形。
故答案为:平行四边形。
查看更多完整答案,请扫码查看


