16. 如图,由6个小正方形组成的$2×3$网格中,任意选取5个小正方形并涂黑,则黑色部分组成的图形是轴对称图形的概率是
$\frac{1}{3}$
.
答案:
解:从6个小正方形中任意选取5个涂黑,共有6种情况(即分别保留1个小正方形不涂黑)。
要使黑色部分组成轴对称图形,需保留的白色小正方形位置满足:
1. 第一行中间;
2. 第二行中间;
3. 第一行左、右两格之一;
4. 第二行左、右两格之一。
经分析,符合条件的情况有2种(保留第一行中间或第二行中间的小正方形)。
概率为$\frac{2}{6}=\frac{1}{3}$。
$\frac{1}{3}$
要使黑色部分组成轴对称图形,需保留的白色小正方形位置满足:
1. 第一行中间;
2. 第二行中间;
3. 第一行左、右两格之一;
4. 第二行左、右两格之一。
经分析,符合条件的情况有2种(保留第一行中间或第二行中间的小正方形)。
概率为$\frac{2}{6}=\frac{1}{3}$。
$\frac{1}{3}$
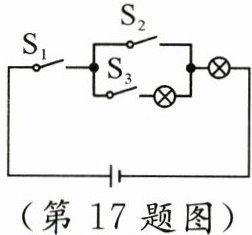
17. 如图,电路连接完好,且各元件工作正常,随机闭合开关$S_{1}$,$S_{2}$,$S_{3}$中的两个,能让两个小灯泡同时发光的概率是______.

$\frac{1}{3}$
答案:
解:随机闭合开关$S_{1}$,$S_{2}$,$S_{3}$中的两个,所有可能的情况有:$(S_{1},S_{2})$、$(S_{1},S_{3})$、$(S_{2},S_{3})$,共3种。
分析各情况:
- 闭合$S_{1}$和$S_{2}$:电流从电源正极出发,经$S_{1}$、$S_{2}$后直接回到电源负极,右边小灯泡被短路,只有左边小灯泡发光,不符合题意。
- 闭合$S_{1}$和$S_{3}$:电流从电源正极出发,经$S_{1}$后分为两支,一支经$S_{3}$、左边小灯泡,另一支经右边小灯泡,然后汇合回到电源负极,两个小灯泡同时发光,符合题意。
- 闭合$S_{2}$和$S_{3}$:电路未与电源正极连通,两个小灯泡均不发光,不符合题意。
能让两个小灯泡同时发光的情况有1种,所以概率为$\frac{1}{3}$。
$\frac{1}{3}$
分析各情况:
- 闭合$S_{1}$和$S_{2}$:电流从电源正极出发,经$S_{1}$、$S_{2}$后直接回到电源负极,右边小灯泡被短路,只有左边小灯泡发光,不符合题意。
- 闭合$S_{1}$和$S_{3}$:电流从电源正极出发,经$S_{1}$后分为两支,一支经$S_{3}$、左边小灯泡,另一支经右边小灯泡,然后汇合回到电源负极,两个小灯泡同时发光,符合题意。
- 闭合$S_{2}$和$S_{3}$:电路未与电源正极连通,两个小灯泡均不发光,不符合题意。
能让两个小灯泡同时发光的情况有1种,所以概率为$\frac{1}{3}$。
$\frac{1}{3}$
18. 现有四张正面分别标有数字-1,1,2,3的不透明卡片,它们除数字外其余完全相同. 将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张,记下数字,前后两次抽取的数字分别记为$m$,$n$,则点$P(m,n)$在第二象限的概率为______
$\frac{3}{16}$
.
答案:
解:列表如下:
| 第一次\第二次 | -1 | 1 | 2 | 3 |
| --- | --- | --- | --- | --- |
| -1 | (-1,-1) | (-1,1) | (-1,2) | (-1,3) |
| 1 | (1,-1) | (1,1) | (1,2) | (1,3) |
| 2 | (2,-1) | (2,1) | (2,2) | (2,3) |
| 3 | (3,-1) | (3,1) | (3,2) | (3,3) |
共有16种等可能的结果,其中点P(m,n)在第二象限的结果有(-1,1),(-1,2),(-1,3),共3种。
所以点P(m,n)在第二象限的概率为$\frac{3}{16}$。
$\frac{3}{16}$
| 第一次\第二次 | -1 | 1 | 2 | 3 |
| --- | --- | --- | --- | --- |
| -1 | (-1,-1) | (-1,1) | (-1,2) | (-1,3) |
| 1 | (1,-1) | (1,1) | (1,2) | (1,3) |
| 2 | (2,-1) | (2,1) | (2,2) | (2,3) |
| 3 | (3,-1) | (3,1) | (3,2) | (3,3) |
共有16种等可能的结果,其中点P(m,n)在第二象限的结果有(-1,1),(-1,2),(-1,3),共3种。
所以点P(m,n)在第二象限的概率为$\frac{3}{16}$。
$\frac{3}{16}$
19. (8分)在一个不透明的袋子中装有仅颜色不同的20个小球,其中白球8个,黑球12个.
(1)先从袋子中取出$a(a>1)$个白球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A. 当事件A是必然事件时,$a=$
(2)先从袋子中取出$a$个白球,再放入$a$个一样的黑球并摇匀,若随机摸出1个球是白球的概率等于$\frac{3}{10}$,求$a$的值.
(1)先从袋子中取出$a(a>1)$个白球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A. 当事件A是必然事件时,$a=$
8
;(2)先从袋子中取出$a$个白球,再放入$a$个一样的黑球并摇匀,若随机摸出1个球是白球的概率等于$\frac{3}{10}$,求$a$的值.
根据题意,得 $\frac{8 - a}{20} = \frac{3}{10}$,解得 $a = 2$。
答案:
(1) 8;
(2) 根据题意,得 $\frac{8 - a}{20} = \frac{3}{10}$,解得 $a = 2$。
(1) 8;
(2) 根据题意,得 $\frac{8 - a}{20} = \frac{3}{10}$,解得 $a = 2$。
20. (8分)一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球、8个黑球、7个红球.
(1)若从袋中摸出一个球,刚好是黄球的概率是
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出1个黑球的概率是$\frac{1}{3}$,求从袋中取出黑球的个数.
(1)若从袋中摸出一个球,刚好是黄球的概率是
$\frac{1}{4}$
;(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出1个黑球的概率是$\frac{1}{3}$,求从袋中取出黑球的个数.
(2) 设从袋中取出黑球的个数为$x$。根据题意,得
$\frac{8 - x}{20 - x} = \frac{1}{3}$
$3(8 - x) = 20 - x$
$24 - 3x = 20 - x$
$-3x + x = 20 - 24$
$-2x = -4$
$x = 2$
经检验,$x = 2$是原方程的解,且符合题意。
答:从袋中取出黑球的个数为2。
$\frac{8 - x}{20 - x} = \frac{1}{3}$
$3(8 - x) = 20 - x$
$24 - 3x = 20 - x$
$-3x + x = 20 - 24$
$-2x = -4$
$x = 2$
经检验,$x = 2$是原方程的解,且符合题意。
答:从袋中取出黑球的个数为2。
答案:
(1) $\frac{1}{4}$
(2) 设从袋中取出黑球的个数为$x$。根据题意,得
$\frac{8 - x}{20 - x} = \frac{1}{3}$
$3(8 - x) = 20 - x$
$24 - 3x = 20 - x$
$-3x + x = 20 - 24$
$-2x = -4$
$x = 2$
经检验,$x = 2$是原方程的解,且符合题意。
答:从袋中取出黑球的个数为2。
(1) $\frac{1}{4}$
(2) 设从袋中取出黑球的个数为$x$。根据题意,得
$\frac{8 - x}{20 - x} = \frac{1}{3}$
$3(8 - x) = 20 - x$
$24 - 3x = 20 - x$
$-3x + x = 20 - 24$
$-2x = -4$
$x = 2$
经检验,$x = 2$是原方程的解,且符合题意。
答:从袋中取出黑球的个数为2。
查看更多完整答案,请扫码查看


