1. 已知$\odot O$的直径为 3 cm,点 P 到圆心的距离$OP = 2$ cm,则点 P(
A.在$\odot O$外
B.在$\odot O$上
C.在$\odot O$内
D.不能确定
A
)A.在$\odot O$外
B.在$\odot O$上
C.在$\odot O$内
D.不能确定
答案:
解:$\odot O$的直径为3cm,所以半径$r = \frac{3}{2} = 1.5$cm。
点P到圆心的距离$OP = 2$cm,因为$2 > 1.5$,即$OP > r$。
所以点P在$\odot O$外。
答案:A
点P到圆心的距离$OP = 2$cm,因为$2 > 1.5$,即$OP > r$。
所以点P在$\odot O$外。
答案:A
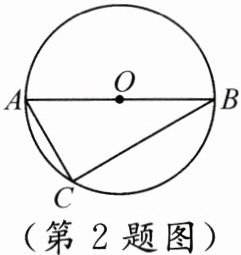
2. 如图,$\odot O的直径AB = 8$,点 C 在$\odot O$上,$\angle ABC = 30^{\circ}$,则 AC 的长是(
A.2
B.$2\sqrt{2}$
C.$2\sqrt{3}$
D.4
D
)
A.2
B.$2\sqrt{2}$
C.$2\sqrt{3}$
D.4
答案:
解:
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角)。
∵AB=8,∠ABC=30°,
∴在Rt△ABC中,AC=AB·sin∠ABC=8×sin30°=8×$\frac{1}{2}$=4。
答案:D
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角)。
∵AB=8,∠ABC=30°,
∴在Rt△ABC中,AC=AB·sin∠ABC=8×sin30°=8×$\frac{1}{2}$=4。
答案:D
3. 如图,EF,CD 是$\odot O$的两条直径,A 是劣弧$\widehat{DF}$的中点. 若$\angle EOD = 32^{\circ}$,则$\angle CDA$的度数为(
A.$37^{\circ}$
B.$74^{\circ}$
C.$53^{\circ}$
D.$63^{\circ}$
C
)A.$37^{\circ}$
B.$74^{\circ}$
C.$53^{\circ}$
D.$63^{\circ}$
答案:
解:
∵EF是⊙O的直径,∠EOD=32°,
∴∠DOF=180°-∠EOD=180°-32°=148°.
∵A是劣弧$\widehat{DF}$的中点,
∴$\widehat{DA}=\widehat{AF}=\frac{1}{2}\widehat{DF}$,
∴∠DOA=$\frac{1}{2}$∠DOF=$\frac{1}{2}×148°=74°$.
∵OA=OD(同圆半径相等),
∴△OAD是等腰三角形,∠ODA=∠OAD.
∴∠ODA=$\frac{1}{2}(180°-∠DOA)=\frac{1}{2}(180°-74°)=53°$.
即∠CDA=53°.
答案:C
∵EF是⊙O的直径,∠EOD=32°,
∴∠DOF=180°-∠EOD=180°-32°=148°.
∵A是劣弧$\widehat{DF}$的中点,
∴$\widehat{DA}=\widehat{AF}=\frac{1}{2}\widehat{DF}$,
∴∠DOA=$\frac{1}{2}$∠DOF=$\frac{1}{2}×148°=74°$.
∵OA=OD(同圆半径相等),
∴△OAD是等腰三角形,∠ODA=∠OAD.
∴∠ODA=$\frac{1}{2}(180°-∠DOA)=\frac{1}{2}(180°-74°)=53°$.
即∠CDA=53°.
答案:C
4. 如图,CD 是$\odot O$的直径,弦$AB\perp CD$于点 E,连接 BC,BD,下列结论不一定正确的是(
A.$AE = BE$
B.$\widehat{AD} = \widehat{BD}$
C.$OE = DE$
D.$\angle DBC = 90^{\circ}$
C
)A.$AE = BE$
B.$\widehat{AD} = \widehat{BD}$
C.$OE = DE$
D.$\angle DBC = 90^{\circ}$
答案:
解:
∵CD是⊙O的直径,弦AB⊥CD于点E,
∴AE=BE(垂径定理),A正确;
$\widehat{AD}=\widehat{BD}$(垂径定理),B正确;
∵CD是直径,
∴∠DBC=90°(直径所对圆周角是直角),D正确;
OE与DE不一定相等,C不一定正确。
答案:C
∵CD是⊙O的直径,弦AB⊥CD于点E,
∴AE=BE(垂径定理),A正确;
$\widehat{AD}=\widehat{BD}$(垂径定理),B正确;
∵CD是直径,
∴∠DBC=90°(直径所对圆周角是直角),D正确;
OE与DE不一定相等,C不一定正确。
答案:C
5. 如图,在$\triangle ABC$中,$AB = BC = 2$,以 AB 为直径的$\odot O$与 BC 相切于点 B,则 AC 的长是(

A.$\sqrt{2}$
B.$\sqrt{3}$
C.$2\sqrt{2}$
D.$2\sqrt{3}$
C
)
A.$\sqrt{2}$
B.$\sqrt{3}$
C.$2\sqrt{2}$
D.$2\sqrt{3}$
答案:
解:
∵以AB为直径的$\odot O$与BC相切于点B,
∴AB⊥BC,即∠ABC=90°。
∵AB=BC=2,
∴在Rt△ABC中,$AC=\sqrt{AB^2 + BC^2}=\sqrt{2^2 + 2^2}=2\sqrt{2}$。
答案:C
∵以AB为直径的$\odot O$与BC相切于点B,
∴AB⊥BC,即∠ABC=90°。
∵AB=BC=2,
∴在Rt△ABC中,$AC=\sqrt{AB^2 + BC^2}=\sqrt{2^2 + 2^2}=2\sqrt{2}$。
答案:C
6. 如图,AB 为半圆 O 的直径,C,D 是半圆 O 上的两点,$\angle BAC = 20^{\circ}$,$\widehat{AD} = \widehat{CD}$,则$\angle DAC$的度数为(
A.$40^{\circ}$
B.$35^{\circ}$
C.$30^{\circ}$
D.$25^{\circ}$
B
)A.$40^{\circ}$
B.$35^{\circ}$
C.$30^{\circ}$
D.$25^{\circ}$
答案:
B
7. 如图,半径为 5 的$\odot A$与 y 轴交于点$B(0,2)$,$C(0,10)$,则点 A 的横坐标为(
A.-3
B.3
C.4
D.6
B
)A.-3
B.3
C.4
D.6
答案:
解:设点A的坐标为$(x,y)$。
因为$\odot A$的半径为5,且与y轴交于点$B(0,2)$,$C(0,10)$,
所以$AB=AC=5$。
根据两点间距离公式可得:
$\sqrt{(x-0)^2+(y-2)^2}=5$,$\sqrt{(x-0)^2+(y-10)^2}=5$。
即$x^2+(y-2)^2=25$,$x^2+(y-10)^2=25$。
两式相减得:$(y-2)^2-(y-10)^2=0$,
展开得:$y^2 - 4y + 4 - (y^2 - 20y + 100) = 0$,
化简得:$16y - 96 = 0$,解得$y=6$。
将$y=6$代入$x^2+(6-2)^2=25$,得$x^2 + 16 = 25$,$x^2=9$,解得$x=\pm3$。
由图可知点A在第一象限,所以$x=3$。
答案:B
因为$\odot A$的半径为5,且与y轴交于点$B(0,2)$,$C(0,10)$,
所以$AB=AC=5$。
根据两点间距离公式可得:
$\sqrt{(x-0)^2+(y-2)^2}=5$,$\sqrt{(x-0)^2+(y-10)^2}=5$。
即$x^2+(y-2)^2=25$,$x^2+(y-10)^2=25$。
两式相减得:$(y-2)^2-(y-10)^2=0$,
展开得:$y^2 - 4y + 4 - (y^2 - 20y + 100) = 0$,
化简得:$16y - 96 = 0$,解得$y=6$。
将$y=6$代入$x^2+(6-2)^2=25$,得$x^2 + 16 = 25$,$x^2=9$,解得$x=\pm3$。
由图可知点A在第一象限,所以$x=3$。
答案:B
8. 若圆锥的底面半径为 3 cm,母线长为 8 cm,则这个圆锥的侧面积为(
A.$12$ cm^2
B.$24$ cm^2
C.$12\pi$ cm^2
D.$24\pi$ cm^2
D
)A.$12$ cm^2
B.$24$ cm^2
C.$12\pi$ cm^2
D.$24\pi$ cm^2
答案:
解:圆锥侧面积公式为 $ S = \pi r l $(其中 $ r $ 为底面半径,$ l $ 为母线长)。
已知 $ r = 3 \, \text{cm} $,$ l = 8 \, \text{cm} $,
则 $ S = \pi × 3 × 8 = 24\pi \, \text{cm}^2 $。
答案:D
已知 $ r = 3 \, \text{cm} $,$ l = 8 \, \text{cm} $,
则 $ S = \pi × 3 × 8 = 24\pi \, \text{cm}^2 $。
答案:D
查看更多完整答案,请扫码查看


