24.(10 分)【问题解决】
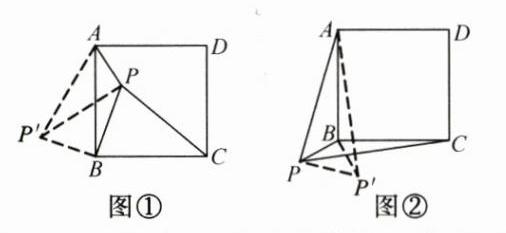
一节数学课上,老师提出了这样一个问题:如图①,点 $P$ 是正方形 $ABCD$ 内一点,$PA = 1$,$PB = 2$,$PC = 3$,你能求出 $\angle APB$ 的度数吗?小明通过观察、分析、思考,形成了如下思路:
思路一:将 $\triangle BPC$ 绕点 $B$ 逆时针旋转 $90^{\circ}$,得到 $\triangle BP'A$,连接 $PP'$,求出 $\angle APB$ 的度数;
思路二:将 $\triangle APB$ 绕点 $B$ 顺时针旋转 $90^{\circ}$,得到 $\triangle CP'B$,连接 $PP'$,求出 $\angle APB$ 的度数。
请参考小明的思路,任选一种写出完整的解答过程;
【类比探究】
如图②,若点 $P$ 是正方形 $ABCD$ 外一点,$PA = 3$,$PB = 1$,$PC= \sqrt{11}$,求 $\angle APB$ 的度数。

一节数学课上,老师提出了这样一个问题:如图①,点 $P$ 是正方形 $ABCD$ 内一点,$PA = 1$,$PB = 2$,$PC = 3$,你能求出 $\angle APB$ 的度数吗?小明通过观察、分析、思考,形成了如下思路:
思路一:将 $\triangle BPC$ 绕点 $B$ 逆时针旋转 $90^{\circ}$,得到 $\triangle BP'A$,连接 $PP'$,求出 $\angle APB$ 的度数;
思路二:将 $\triangle APB$ 绕点 $B$ 顺时针旋转 $90^{\circ}$,得到 $\triangle CP'B$,连接 $PP'$,求出 $\angle APB$ 的度数。
请参考小明的思路,任选一种写出完整的解答过程;
【类比探究】
如图②,若点 $P$ 是正方形 $ABCD$ 外一点,$PA = 3$,$PB = 1$,$PC= \sqrt{11}$,求 $\angle APB$ 的度数。

答案:
解:【问题解决】思路一:如图①。将 $\triangle BPC$ 绕点 $B$ 逆时针旋转 $90^{\circ}$,得到 $\triangle BP'A$,连接 $PP'$,$\therefore \angle PBP' = 90^{\circ}$,$BP' = BP = 2$,$AP' = CP = 3$。在 $\mathrm{Rt} \triangle BPP'$ 中,$\because BP = BP' =2$,$\therefore \angle BPP' = 45^{\circ}$。由勾股定理,得 $PP' = \sqrt{BP^2 + BP'^2} = \sqrt{2^2 + 2^2} = 2\sqrt{2}$。$\because AP = 1$,$\therefore AP^2 + PP'^2 = 1 + 8 = 9$。$\because AP'^2 = 3^2 = 9$,$\therefore AP^2 + PP'^2 = AP'^2$,$\therefore \triangle APP'$ 是直角三角形,且 $\angle APP' = 90^{\circ}$,$\therefore \angle APB = \angle APP' + \angle BPP' = 90^{\circ} + 45^{\circ} = 135^{\circ}$;思路二:求解过程略;
【类比探究】如图②,将 $\triangle BPC$ 绕点 $B$ 逆时针旋转 $90^{\circ}$,得到 $\triangle BP'A$,连接 $PP'$,$\therefore \angle PBP' = 90^{\circ}$,$BP' = BP = 1$,$AP' = CP = \sqrt{11}$,$\therefore \angle BPP' = 45^{\circ}$。在 $\mathrm{Rt} \triangle BPP'$ 中,由勾股定理,得 $PP' = \sqrt{BP^2 + BP'^2} = \sqrt{1^2 + 1^2} = \sqrt{2}$。$\because AP = 3$,$\therefore AP^2 + PP'^2 = 9 + 2 = 11$。$\because AP'^2 = (\sqrt{11})^2 = 11$,$\therefore AP^2 + PP'^2 = AP'^2$,$\therefore \triangle APP'$ 是直角三角形,且 $\angle APP' = 90^{\circ}$,$\therefore \angle APB = \angle APP' - \angle BPP' = 90^{\circ} - 45^{\circ} = 45^{\circ}$。
解:【问题解决】思路一:如图①。将 $\triangle BPC$ 绕点 $B$ 逆时针旋转 $90^{\circ}$,得到 $\triangle BP'A$,连接 $PP'$,$\therefore \angle PBP' = 90^{\circ}$,$BP' = BP = 2$,$AP' = CP = 3$。在 $\mathrm{Rt} \triangle BPP'$ 中,$\because BP = BP' =2$,$\therefore \angle BPP' = 45^{\circ}$。由勾股定理,得 $PP' = \sqrt{BP^2 + BP'^2} = \sqrt{2^2 + 2^2} = 2\sqrt{2}$。$\because AP = 1$,$\therefore AP^2 + PP'^2 = 1 + 8 = 9$。$\because AP'^2 = 3^2 = 9$,$\therefore AP^2 + PP'^2 = AP'^2$,$\therefore \triangle APP'$ 是直角三角形,且 $\angle APP' = 90^{\circ}$,$\therefore \angle APB = \angle APP' + \angle BPP' = 90^{\circ} + 45^{\circ} = 135^{\circ}$;思路二:求解过程略;

【类比探究】如图②,将 $\triangle BPC$ 绕点 $B$ 逆时针旋转 $90^{\circ}$,得到 $\triangle BP'A$,连接 $PP'$,$\therefore \angle PBP' = 90^{\circ}$,$BP' = BP = 1$,$AP' = CP = \sqrt{11}$,$\therefore \angle BPP' = 45^{\circ}$。在 $\mathrm{Rt} \triangle BPP'$ 中,由勾股定理,得 $PP' = \sqrt{BP^2 + BP'^2} = \sqrt{1^2 + 1^2} = \sqrt{2}$。$\because AP = 3$,$\therefore AP^2 + PP'^2 = 9 + 2 = 11$。$\because AP'^2 = (\sqrt{11})^2 = 11$,$\therefore AP^2 + PP'^2 = AP'^2$,$\therefore \triangle APP'$ 是直角三角形,且 $\angle APP' = 90^{\circ}$,$\therefore \angle APB = \angle APP' - \angle BPP' = 90^{\circ} - 45^{\circ} = 45^{\circ}$。
查看更多完整答案,请扫码查看


