21. (9分)已知直线$ y = 2 x + 4 $交x轴于点A,交y轴于点B,点C,D分别是点A,B关于原点的对称点.
(1)求直线CD的解析式;
(2)求四边形ABCD的面积.
(1)求直线CD的解析式;
(2)求四边形ABCD的面积.
答案:
(1) 解:令 $ y = 0 $,则 $ 2x + 4 = 0 $,解得 $ x = -2 $,所以 $ A(-2, 0) $;令 $ x = 0 $,则 $ y = 4 $,所以 $ B(0, 4) $。
因为点 $ C $,$ D $ 分别是点 $ A $,$ B $ 关于原点的对称点,所以 $ C(2, 0) $,$ D(0, -4) $。
设直线 $ CD $ 的解析式为 $ y = kx + b $,将 $ C(2, 0) $,$ D(0, -4) $ 代入得:
$\begin{cases} 2k + b = 0 \\ b = -4 \end{cases}$,解得 $\begin{cases} k = 2 \\ b = -4 \end{cases}$。
所以直线 $ CD $ 的解析式为 $ y = 2x - 4 $。
(2) 解:$ AC = |2 - (-2)| = 4 $,$ OB = 4 $,$ OD = 4 $。
$ S_{\text{四边形}ABCD} = S_{\triangle ABC} + S_{\triangle ADC} = \frac{1}{2} × AC × OB + \frac{1}{2} × AC × OD = \frac{1}{2} × 4 × 4 + \frac{1}{2} × 4 × 4 = 8 + 8 = 16 $。
(1) 解:令 $ y = 0 $,则 $ 2x + 4 = 0 $,解得 $ x = -2 $,所以 $ A(-2, 0) $;令 $ x = 0 $,则 $ y = 4 $,所以 $ B(0, 4) $。
因为点 $ C $,$ D $ 分别是点 $ A $,$ B $ 关于原点的对称点,所以 $ C(2, 0) $,$ D(0, -4) $。
设直线 $ CD $ 的解析式为 $ y = kx + b $,将 $ C(2, 0) $,$ D(0, -4) $ 代入得:
$\begin{cases} 2k + b = 0 \\ b = -4 \end{cases}$,解得 $\begin{cases} k = 2 \\ b = -4 \end{cases}$。
所以直线 $ CD $ 的解析式为 $ y = 2x - 4 $。
(2) 解:$ AC = |2 - (-2)| = 4 $,$ OB = 4 $,$ OD = 4 $。
$ S_{\text{四边形}ABCD} = S_{\triangle ABC} + S_{\triangle ADC} = \frac{1}{2} × AC × OB + \frac{1}{2} × AC × OD = \frac{1}{2} × 4 × 4 + \frac{1}{2} × 4 × 4 = 8 + 8 = 16 $。
22. (9分)如图,$ \triangle A B C 经过某种变换后得到 \triangle D E F $,点A,B,C的对应点分别是点D,E,F,请观察它们之间的关系,完成以下问题:
(1)请分别写出点A,D的坐标:A
(2)若$ \triangle A B C $内任意一点M的坐标是$ ( x, y ) $,点M经过这种变换后得到点N,则点N的坐标是
(3)在上述变换情况下,点$ P ( a + 3, - b + 6 ) 与点 Q ( 2 b - 3, - 2 a ) $为对应点,求$ a + b $的值.
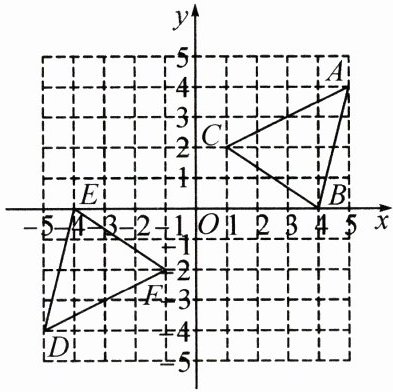
(1)请分别写出点A,D的坐标:A
(5,4)
,D(-5,-4)
;(2)若$ \triangle A B C $内任意一点M的坐标是$ ( x, y ) $,点M经过这种变换后得到点N,则点N的坐标是
(-x,-y)
;(3)在上述变换情况下,点$ P ( a + 3, - b + 6 ) 与点 Q ( 2 b - 3, - 2 a ) $为对应点,求$ a + b $的值.
解:根据题意,得$\begin{cases}a + 3 = - (2b - 3)\\-b + 6 = - (-2a)\end{cases}$
化简得$\begin{cases}a + 2b = 0\\-2a - b = -6\end{cases}$
解得$\begin{cases}a = 4\\b = -2\end{cases}$
$\therefore a + b = 4 + (-2) = 2$
化简得$\begin{cases}a + 2b = 0\\-2a - b = -6\end{cases}$
解得$\begin{cases}a = 4\\b = -2\end{cases}$
$\therefore a + b = 4 + (-2) = 2$

答案:
(1) $(5,4)$; $(-5,-4)$
(2) $(-x,-y)$
(3) 解:根据题意,得$\begin{cases}a + 3 = - (2b - 3)\\-b + 6 = - (-2a)\end{cases}$
化简得$\begin{cases}a + 2b = 0\\-2a - b = -6\end{cases}$
解得$\begin{cases}a = 4\\b = -2\end{cases}$
$\therefore a + b = 4 + (-2) = 2$
(1) $(5,4)$; $(-5,-4)$
(2) $(-x,-y)$
(3) 解:根据题意,得$\begin{cases}a + 3 = - (2b - 3)\\-b + 6 = - (-2a)\end{cases}$
化简得$\begin{cases}a + 2b = 0\\-2a - b = -6\end{cases}$
解得$\begin{cases}a = 4\\b = -2\end{cases}$
$\therefore a + b = 4 + (-2) = 2$
查看更多完整答案,请扫码查看


