9. 如图,AB 为$\odot O$的直径,PB,PC 分别与$\odot O$相切于点 B,C,过点 C 作 AB 的垂线,垂足为 E,交$\odot O$于点 D. 若$CD = PB = 2\sqrt{3}$,则 BE 的长为(
A.1
B.2
C.3
D.4
C
)A.1
B.2
C.3
D.4
答案:
C
10. 如图,在菱形 ABCD 中,$\angle BAD = 60^{\circ}$,O 为对角线的交点. 将菱形 ABCD 绕点 O 逆时针旋转$90^{\circ}得到菱形A'B'C'D'$,两个菱形的公共点为 E,F,G,H. 对八边形$BFB'GDHD'E$给出下面四个结论:①该八边形各边长都相等;②该八边形各内角都相等;③点 O 到该八边形各顶点的距离都相等;④点 O 到该八边形各边所在直线的距离都相等. 上述结论中,所有正确结论的序号是(
A.①③
B.①④
C.②③
D.②④
B
)A.①③
B.①④
C.②③
D.②④
答案:
解:
① 由菱形性质及旋转对称性,八边形各边均为两菱形边的交点连线,可证各边长相等;
② 八边形内角包含菱形内角(60°、120°)及旋转后形成的新角,内角不都相等;
③ 点O到各顶点距离为菱形对角线的一半或交点连线长度,不都相等;
④ 点O为两菱形中心,由对称性知到各边所在直线距离相等。
正确结论序号:①④
答案:B
① 由菱形性质及旋转对称性,八边形各边均为两菱形边的交点连线,可证各边长相等;
② 八边形内角包含菱形内角(60°、120°)及旋转后形成的新角,内角不都相等;
③ 点O到各顶点距离为菱形对角线的一半或交点连线长度,不都相等;
④ 点O为两菱形中心,由对称性知到各边所在直线距离相等。
正确结论序号:①④
答案:B
11. 如图,在$\odot O$中,直径$CD\perp$弦 AB,垂足为 E,已知$AB = 6$,$OE = 4$,则 CD 的长为______.
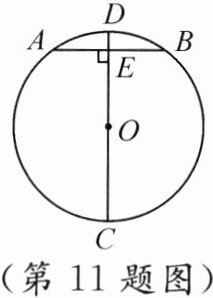

10
答案:
解:连接OA。
因为CD是直径且CD⊥AB,AB=6,所以AE=AB/2=3。
设OA=OC=OD=r(r为半径),则OE=4,在Rt△AOE中,由勾股定理得:
OA²=AE²+OE²,即r²=3²+4²=25,解得r=5。
所以CD=2r=10。
答案:10
因为CD是直径且CD⊥AB,AB=6,所以AE=AB/2=3。
设OA=OC=OD=r(r为半径),则OE=4,在Rt△AOE中,由勾股定理得:
OA²=AE²+OE²,即r²=3²+4²=25,解得r=5。
所以CD=2r=10。
答案:10
12. 将一个圆分成三个扇形 A,B,C,它们的面积之比为$1:3:5$,则面积最小的扇形的圆心角度数为
$40^{\circ}$
.
答案:
解:设扇形A、B、C的圆心角分别为$x$、$3x$、$5x$。
因为整个圆的圆心角为$360^{\circ}$,所以$x + 3x + 5x = 360^{\circ}$,
解得$9x = 360^{\circ}$,$x = 40^{\circ}$。
$40^{\circ}$
因为整个圆的圆心角为$360^{\circ}$,所以$x + 3x + 5x = 360^{\circ}$,
解得$9x = 360^{\circ}$,$x = 40^{\circ}$。
$40^{\circ}$
13. 如图,AB 是$\odot O$的直径,C,D 是$\odot O$上两点,BA 平分$\angle CBD$. 若$\angle AOD = 50^{\circ}$,则$\angle A$的度数为______
65°
.
答案:
65°
14. 如图,木工用角尺的短边紧靠$\odot O$于点 A,长边与$\odot O$相切于点 B,角尺的直角顶点为 C. 已知$AC = 6$ cm,$CB = 8$ cm,则$\odot O$的半径为
$\frac{25}{3}$
cm.
答案:
解:连接 $OA$、$OB$,过点 $A$ 作 $AD \perp OB$ 于点 $D$。
因为角尺短边紧靠 $\odot O$ 于点 $A$,长边与 $\odot O$ 相切于点 $B$,所以 $OA \perp AC$,$OB \perp BC$。
又因为 $\angle C = 90^\circ$,所以四边形 $ACBD$ 是矩形,因此 $AD = CB = 8$ cm,$BD = AC = 6$ cm。
设 $\odot O$ 的半径为 $r$ cm,则 $OA = OB = r$ cm,$OD = OB - BD = (r - 6)$ cm。
在 $Rt\triangle AOD$ 中,由勾股定理得:$OA^2 = OD^2 + AD^2$,即 $r^2 = (r - 6)^2 + 8^2$。
解得 $r = \frac{25}{3}$。
$\frac{25}{3}$
因为角尺短边紧靠 $\odot O$ 于点 $A$,长边与 $\odot O$ 相切于点 $B$,所以 $OA \perp AC$,$OB \perp BC$。
又因为 $\angle C = 90^\circ$,所以四边形 $ACBD$ 是矩形,因此 $AD = CB = 8$ cm,$BD = AC = 6$ cm。
设 $\odot O$ 的半径为 $r$ cm,则 $OA = OB = r$ cm,$OD = OB - BD = (r - 6)$ cm。
在 $Rt\triangle AOD$ 中,由勾股定理得:$OA^2 = OD^2 + AD^2$,即 $r^2 = (r - 6)^2 + 8^2$。
解得 $r = \frac{25}{3}$。
$\frac{25}{3}$
15. 如图,正六边形 ABCDEF 内接于$\odot O$,点 P 是$\widehat{CD}$上的任意一点,则$\angle APB$的大小是______.
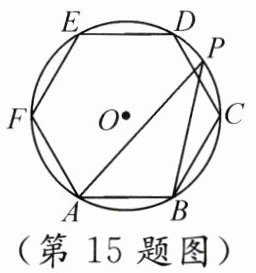

30°
答案:
连接OA、OB。
因为正六边形ABCDEF内接于⊙O,所以中心角∠AOB = 360°÷6 = 60°。
点P在⊙O上,∠APB是弧AB所对的圆周角,根据圆周角定理,∠APB = 1/2∠AOB = 1/2×60° = 30°。
30°
因为正六边形ABCDEF内接于⊙O,所以中心角∠AOB = 360°÷6 = 60°。
点P在⊙O上,∠APB是弧AB所对的圆周角,根据圆周角定理,∠APB = 1/2∠AOB = 1/2×60° = 30°。
30°
查看更多完整答案,请扫码查看


