《2025年名师测控九年级数学上册人教版》

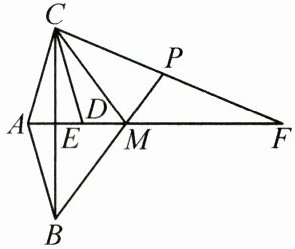
23. (10分)如图,$ \triangle A B M 与 \triangle A C M $关于直线AF成轴对称,$ \triangle A B E 与 \triangle D C E $关于点E成中心对称,点E,D,M都在线段AF上,BM的延长线交CF于点P.
(1)求证：$ A C = C D $；
(2)若$ \angle B A C = 2 \angle M P C $,请你判断$ \angle F 与 \angle M C D $的数量关系,并说明理由.

答案：
(1) 证明：
∵△ABM与△ACM关于直线AF成轴对称，
∴△ABM≌△ACM，
∴AB=AC。
∵△ABE与△DCE关于点E成中心对称，
∴△ABE≌△DCE，
∴AB=CD，
∴AC=CD。
(2) ∠F=∠MCD。
理由如下：
由
(1)得∠BAE=∠CAE=∠CDE，∠CMA=∠BMA。
∵∠BAC=2∠MPC，设∠MPC=α，则∠BAC=2α，
∴∠BAE=∠CAE=∠CDE=α。
设∠BMA=β，则∠PMF=∠CMA=β，
∴∠F=∠MPC-∠PMF=α-β，
∠MCD=∠CDE-∠DMC=α-β，
∴∠F=∠MCD。

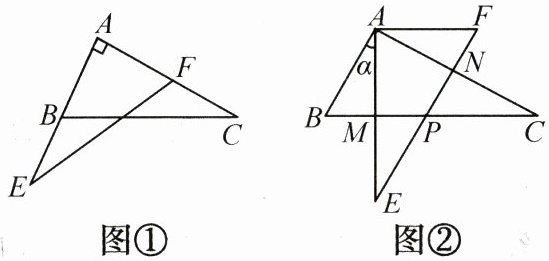
24. (10分)某校九年级数学兴趣小组在学习探究过程中,将两块完全相同的且含$ 60 ^ { \circ } $角的直角三角尺ABC与AFE按如图①所示位置放置. 现将$ \mathrm { Rt } \triangle A E F $绕点A按逆时针方向旋转角$ \alpha $($ 0 ^ { \circ } ＜ \alpha ＜ 90 ^ { \circ } $),如图②,AE与BC相交于点M,AC与EF相交于点N,BC与EF相交于点P.
(1)求证：$ A M = A N $；
(2)当旋转角$ \alpha = 30 ^ { \circ } $时,四边形ABPF是什么特殊四边形？请说明理由.

答案：
(1)证明：由旋转的性质知$\angle BAM = \angle FAN$。
$\because AB = AF$，$\angle B = \angle F = 60^\circ$，
$\therefore \triangle ABM \cong \triangle AFN(ASA)$，
$\therefore AM = AN$。
(2)解：当旋转角$\alpha = 30^\circ$时，四边形$ABPF$是菱形。理由如下：
$\because \alpha = 30^\circ$，
$\therefore \angle BAF = \angle FAE + \angle BAM = 90^\circ + 30^\circ = 120^\circ$。
$\because \angle B = \angle F = 60^\circ$，
$\therefore \angle B + \angle BAF = 180^\circ$，$\angle F + \angle BAF = 180^\circ$，
$\therefore AF // BP$，$AB // FP$，
$\therefore$四边形$ABPF$是平行四边形。
又$\because AB = AF$，
$\therefore$四边形$ABPF$是菱形。