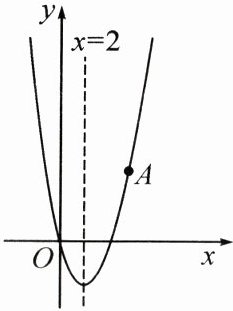
25. (12 分)如图,抛物线经过点 $ O(0, 0) $,$ A(5, 5) $,且它的对称轴为直线 $ x = 2 $。
(1)求此抛物线的解析式;
(2)若点 $ B $ 是抛物线对称轴上的一点,且点 $ B $ 在第一象限,当 $ \triangle OAB $ 的面积为 $ 15 $ 时,求点 $ B $ 的坐标;
(3)在(2)的条件下,$ P $ 是抛物线上的动点,当 $ PA - PB $ 的值最大时,求点 $ P $ 的坐标以及 $ PA - PB $ 的最大值。
(1)求此抛物线的解析式;
(2)若点 $ B $ 是抛物线对称轴上的一点,且点 $ B $ 在第一象限,当 $ \triangle OAB $ 的面积为 $ 15 $ 时,求点 $ B $ 的坐标;
(3)在(2)的条件下,$ P $ 是抛物线上的动点,当 $ PA - PB $ 的值最大时,求点 $ P $ 的坐标以及 $ PA - PB $ 的最大值。

答案:
解:
(1) $\because$ 抛物线过点 $O(0,0)$,$A(5,5)$,且它的对称轴为直线 $x=2$,$\therefore$ 抛物线与 $x$ 轴的另一个交点的坐标为 $(4,0)$。设抛物线的解析式为 $y=ax(x-4)$,把 $A(5,5)$ 代入,得 $5a=5$,解得 $a=1$,$\therefore y=x(x-4)=x^{2}-4x$,故此抛物线的解析式为 $y=x^{2}-4x$;
(2) $\because$ 点 $B$ 是抛物线对称轴上的一点,且点 $B$ 在第一象限,$\therefore$ 设 $B(2,m)(m>0)$。连接 $OA$,设直线 $OA$ 的解析式为 $y=kx$,则 $5k=5$,解得 $k=1$,$\therefore$ 直线 $OA$ 的解析式为 $y=x$。设直线 $OA$ 与抛物线对称轴交于点 $H$,如答图①,则 $H(2,2)$,$\therefore BH=|m-2|$。$\because S_{\triangle OAB}=15$,$\therefore \frac{1}{2}×|m-2|×5=15$,解得 $m=8$ 或 $-4$。$\because m>0$,$\therefore m=8$,$\therefore$ 点 $B$ 的坐标为 $(2,8)$;
(3) 设直线 $AB$ 的解析式为 $y=cx+d$,把 $A(5,5)$,$B(2,8)$ 代入,得 $\begin{cases}5c+d=5,\\2c+d=8,\end{cases}$ 解得 $\begin{cases}c=-1,\\d=10,\end{cases}$ $\therefore$ 直线 $AB$ 的解析式为 $y=-x+10$。当 $PA-PB$ 的值最大时,$A$、$B$、$P$ 在同一条直线上,如答图②。$\because P$ 是抛物线上的动点,联立 $\begin{cases}y=-x+10,\\y=x^{2}-4x,\end{cases}$ 解得 $\begin{cases}x_{1}=-2,\\y_{1}=12,\end{cases}$ $\begin{cases}x_{2}=5,\\y_{2}=5\end{cases}$ (舍去)。$\therefore P(-2,12)$,此时,$PA-PB=AB=\sqrt{(5-2)^{2}+(5-8)^{2}}=3\sqrt{2}$。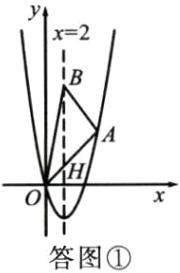

解:
(1) $\because$ 抛物线过点 $O(0,0)$,$A(5,5)$,且它的对称轴为直线 $x=2$,$\therefore$ 抛物线与 $x$ 轴的另一个交点的坐标为 $(4,0)$。设抛物线的解析式为 $y=ax(x-4)$,把 $A(5,5)$ 代入,得 $5a=5$,解得 $a=1$,$\therefore y=x(x-4)=x^{2}-4x$,故此抛物线的解析式为 $y=x^{2}-4x$;
(2) $\because$ 点 $B$ 是抛物线对称轴上的一点,且点 $B$ 在第一象限,$\therefore$ 设 $B(2,m)(m>0)$。连接 $OA$,设直线 $OA$ 的解析式为 $y=kx$,则 $5k=5$,解得 $k=1$,$\therefore$ 直线 $OA$ 的解析式为 $y=x$。设直线 $OA$ 与抛物线对称轴交于点 $H$,如答图①,则 $H(2,2)$,$\therefore BH=|m-2|$。$\because S_{\triangle OAB}=15$,$\therefore \frac{1}{2}×|m-2|×5=15$,解得 $m=8$ 或 $-4$。$\because m>0$,$\therefore m=8$,$\therefore$ 点 $B$ 的坐标为 $(2,8)$;
(3) 设直线 $AB$ 的解析式为 $y=cx+d$,把 $A(5,5)$,$B(2,8)$ 代入,得 $\begin{cases}5c+d=5,\\2c+d=8,\end{cases}$ 解得 $\begin{cases}c=-1,\\d=10,\end{cases}$ $\therefore$ 直线 $AB$ 的解析式为 $y=-x+10$。当 $PA-PB$ 的值最大时,$A$、$B$、$P$ 在同一条直线上,如答图②。$\because P$ 是抛物线上的动点,联立 $\begin{cases}y=-x+10,\\y=x^{2}-4x,\end{cases}$ 解得 $\begin{cases}x_{1}=-2,\\y_{1}=12,\end{cases}$ $\begin{cases}x_{2}=5,\\y_{2}=5\end{cases}$ (舍去)。$\therefore P(-2,12)$,此时,$PA-PB=AB=\sqrt{(5-2)^{2}+(5-8)^{2}}=3\sqrt{2}$。


查看更多完整答案,请扫码查看


