23. (10 分)如图,在$\triangle ABC$中,$AB = 4$,$\angle C = 64^{\circ}$,以 AB 为直径的$\odot O$与 AC 相交于点 D,E 为$\widehat{ABD}$上一点,且$\angle ADE = 40^{\circ}$.
(1)求$\widehat{BE}$的长;
(2)若$\angle EAD = 76^{\circ}$,求证:CB 为$\odot O$的切线.
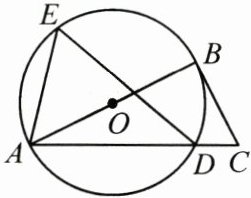
(1)求$\widehat{BE}$的长;
(2)若$\angle EAD = 76^{\circ}$,求证:CB 为$\odot O$的切线.

答案:
(1) 连接 $OE$。
$\because AB$ 是 $\odot O$ 的直径,$AB = 4$,
$\therefore \odot O$ 的半径为 $2$。
$\because \angle ADE = 40^{\circ}$,
$\therefore \angle AOE = 2\angle ADE = 80^{\circ}$(同弧所对的圆心角是圆周角的两倍)。
$\because \angle AOE + \angle BOE = 180^{\circ}$(平角定义),
$\therefore \angle BOE = 180^{\circ} - 80^{\circ} = 100^{\circ}$。
$\therefore \widehat{BE}$ 的长为 $\frac{100 × \pi × 2}{180} = \frac{10}{9}\pi$。
(2) 连接 $BD$。
$\because \angle EAD = 76^{\circ}$,$\angle ADE = 40^{\circ}$,
$\therefore \angle AED = 180^{\circ} - \angle EAD - \angle ADE = 180^{\circ} - 76^{\circ} - 40^{\circ} = 64^{\circ}$(三角形内角和定理)。
$\because \angle ABD = \angle AED = 64^{\circ}$(同弧所对的圆周角相等)。
$\because AB$ 是 $\odot O$ 的直径,
$\therefore \angle ADB = 90^{\circ}$(直径所对的圆周角是直角)。
$\therefore \angle BAC = 90^{\circ} - \angle ABD = 90^{\circ} - 64^{\circ} = 26^{\circ}$。
$\because \angle C = 64^{\circ}$,
$\therefore \angle ABC = 180^{\circ} - \angle C - \angle BAC = 180^{\circ} - 64^{\circ} - 26^{\circ} = 90^{\circ}$(三角形内角和定理)。
$\therefore AB \perp BC$。
$\because OB$ 是 $\odot O$ 的半径,
$\therefore CB$ 为 $\odot O$ 的切线(切线的判定定理)。
(1) 连接 $OE$。
$\because AB$ 是 $\odot O$ 的直径,$AB = 4$,
$\therefore \odot O$ 的半径为 $2$。
$\because \angle ADE = 40^{\circ}$,
$\therefore \angle AOE = 2\angle ADE = 80^{\circ}$(同弧所对的圆心角是圆周角的两倍)。
$\because \angle AOE + \angle BOE = 180^{\circ}$(平角定义),
$\therefore \angle BOE = 180^{\circ} - 80^{\circ} = 100^{\circ}$。
$\therefore \widehat{BE}$ 的长为 $\frac{100 × \pi × 2}{180} = \frac{10}{9}\pi$。
(2) 连接 $BD$。
$\because \angle EAD = 76^{\circ}$,$\angle ADE = 40^{\circ}$,
$\therefore \angle AED = 180^{\circ} - \angle EAD - \angle ADE = 180^{\circ} - 76^{\circ} - 40^{\circ} = 64^{\circ}$(三角形内角和定理)。
$\because \angle ABD = \angle AED = 64^{\circ}$(同弧所对的圆周角相等)。
$\because AB$ 是 $\odot O$ 的直径,
$\therefore \angle ADB = 90^{\circ}$(直径所对的圆周角是直角)。
$\therefore \angle BAC = 90^{\circ} - \angle ABD = 90^{\circ} - 64^{\circ} = 26^{\circ}$。
$\because \angle C = 64^{\circ}$,
$\therefore \angle ABC = 180^{\circ} - \angle C - \angle BAC = 180^{\circ} - 64^{\circ} - 26^{\circ} = 90^{\circ}$(三角形内角和定理)。
$\therefore AB \perp BC$。
$\because OB$ 是 $\odot O$ 的半径,
$\therefore CB$ 为 $\odot O$ 的切线(切线的判定定理)。
24. (10 分)已知在$\triangle AOB$中,$\angle ABO = 30^{\circ}$,AB 为$\odot O$的弦,直线 MN 与$\odot O$相切于点 C.
(1)如图①,若$AB// MN$,直径 CE 与 AB 相交于点 D,求$\angle AOB和\angle BCE$的大小;
(2)如图②,若$OB// MN$,$CG\perp AB$,垂足为 G,CG 与 OB 相交于点 F,$OA = 3$,求线段 OF 的长.
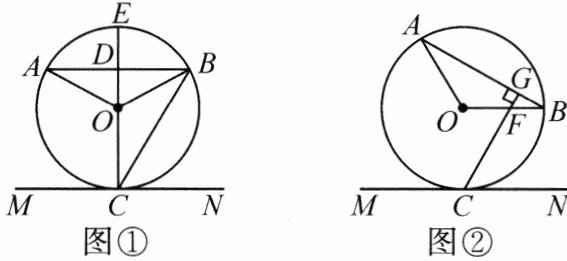
(1)如图①,若$AB// MN$,直径 CE 与 AB 相交于点 D,求$\angle AOB和\angle BCE$的大小;
(2)如图②,若$OB// MN$,$CG\perp AB$,垂足为 G,CG 与 OB 相交于点 F,$OA = 3$,求线段 OF 的长.

答案:
(1) $\because OA=OB$,$\therefore \angle A=\angle ABO$。
$\because \angle A+\angle ABO+\angle AOB=180^{\circ}$,$\angle ABO=30^{\circ}$,
$\therefore \angle AOB=180^{\circ}-2×30^{\circ}=120^{\circ}$。
$\because$ 直线$MN$与$\odot O$相切于点$C$,$CE$为直径,$\therefore \angle ECM=90^{\circ}$。
$\because AB// MN$,$\therefore \angle CDB=\angle ECM=90^{\circ}$,
$\therefore \angle BOE=90^{\circ}-\angle ABO=60^{\circ}$,
$\therefore \angle BCE=\frac{1}{2}\angle BOE=30^{\circ}$。
(2) 连接$OC$。
$\because OB// MN$,直线$MN$与$\odot O$相切于点$C$,$\therefore \angle MCO=\angle COB=90^{\circ}$。
$\because CG\perp AB$,$\therefore \angle FGB=90^{\circ}$。
$\because \angle ABO=30^{\circ}$,$\therefore \angle BFG=90^{\circ}-30^{\circ}=60^{\circ}$,
$\therefore \angle CFO=\angle BFG=60^{\circ}$,$\angle OCF=90^{\circ}-60^{\circ}=30^{\circ}$。
在$Rt\triangle FOC$中,$CF=2OF$,$OC=OA=3$。
由勾股定理得$OF^{2}+3^{2}=(2OF)^{2}$,
即$OF^{2}+9=4OF^{2}$,解得$OF=\sqrt{3}$。
$\angle AOB=120^{\circ}$,$\angle BCE=30^{\circ}$;$OF=\sqrt{3}$。
(1) $\because OA=OB$,$\therefore \angle A=\angle ABO$。
$\because \angle A+\angle ABO+\angle AOB=180^{\circ}$,$\angle ABO=30^{\circ}$,
$\therefore \angle AOB=180^{\circ}-2×30^{\circ}=120^{\circ}$。
$\because$ 直线$MN$与$\odot O$相切于点$C$,$CE$为直径,$\therefore \angle ECM=90^{\circ}$。
$\because AB// MN$,$\therefore \angle CDB=\angle ECM=90^{\circ}$,
$\therefore \angle BOE=90^{\circ}-\angle ABO=60^{\circ}$,
$\therefore \angle BCE=\frac{1}{2}\angle BOE=30^{\circ}$。
(2) 连接$OC$。
$\because OB// MN$,直线$MN$与$\odot O$相切于点$C$,$\therefore \angle MCO=\angle COB=90^{\circ}$。
$\because CG\perp AB$,$\therefore \angle FGB=90^{\circ}$。
$\because \angle ABO=30^{\circ}$,$\therefore \angle BFG=90^{\circ}-30^{\circ}=60^{\circ}$,
$\therefore \angle CFO=\angle BFG=60^{\circ}$,$\angle OCF=90^{\circ}-60^{\circ}=30^{\circ}$。
在$Rt\triangle FOC$中,$CF=2OF$,$OC=OA=3$。
由勾股定理得$OF^{2}+3^{2}=(2OF)^{2}$,
即$OF^{2}+9=4OF^{2}$,解得$OF=\sqrt{3}$。
$\angle AOB=120^{\circ}$,$\angle BCE=30^{\circ}$;$OF=\sqrt{3}$。
查看更多完整答案,请扫码查看


