《2025年名师测控九年级数学上册人教版》

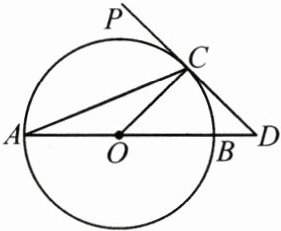
21. (8 分)如图,AB 为$\odot O$的直径,PD 切$\odot O$于点 C,交 AB 的延长线于点 D,且$\angle D = 2\angle A$.
(1)求$\angle D$的度数；
(2)若$CD = 2$,求 BD 的长.

答案：
(1) 解：连接 $OC$，
$\because \angle COD$ 是 $\triangle AOC$ 的外角，
$\therefore \angle COD = 2\angle A$，
$\because \angle D = 2\angle A$，
$\therefore \angle COD = \angle D$，
$\because PD$ 切 $\odot O$ 于点 $C$，
$\therefore OC \perp PD$，即 $\angle OCD = 90^{\circ}$，
在 $\triangle OCD$ 中，$\angle COD + \angle D + \angle OCD = 180^{\circ}$，
$\because \angle COD = \angle D$，$\angle OCD = 90^{\circ}$，
$\therefore 2\angle D + 90^{\circ} = 180^{\circ}$，
$\therefore \angle D = 45^{\circ}$；
(2) 解：由
(1)知 $\angle D = 45^{\circ}$，$\angle OCD = 90^{\circ}$，
$\therefore \triangle OCD$ 是等腰直角三角形，
$\therefore OC = CD$，
$\because CD = 2$，
$\therefore OC = 2$，
在 $Rt\triangle OCD$ 中，由勾股定理得：
$OD = \sqrt{OC^{2} + CD^{2}} = \sqrt{2^{2} + 2^{2}} = 2\sqrt{2}$，
$\because OB = OC = 2$，
$\therefore BD = OD - OB = 2\sqrt{2} - 2$。

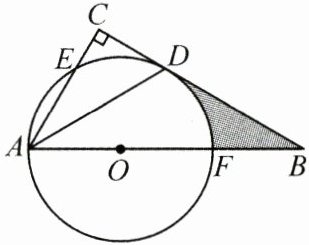
22. (8 分)如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,AD 平分$\angle BAC$交 BC 于点 D,点 O 在 AB 上,以点 O 为圆心,OA 为半径的圆恰好经过点 D,分别交 AC,AB 于点 E,F.
(1)试判断直线 BC 与$\odot O$的位置关系,并说明理由；
(2)若$BD = 2\sqrt{3}$,$AB = 6$,求阴影部分的面积.(结果保留$\pi$)

答案：
(1) 直线$BC$与$\odot O$相切。理由如下：连接$OD$。
$\because OA=OD$，$\therefore \angle OAD=\angle ODA$。
$\because AD$平分$\angle CAB$，$\therefore \angle OAD=\angle CAD$，$\therefore \angle CAD=\angle ODA$，$\therefore AC// OD$。
$\because \angle C=90^{\circ}$，$\therefore \angle ODB=\angle C=90^{\circ}$，即$BC\perp OD$。
$\because OD$为$\odot O$的半径，$\therefore$直线$BC$是$\odot O$的切线。
(2) 设$OA=OD=OF=r$，则$OB=AB-OA=6-r$。
在$Rt\triangle ODB$中，由勾股定理得$OD^{2}+BD^{2}=OB^{2}$，即$r^{2}+(2\sqrt{3})^{2}=(6-r)^{2}$，解得$r=2$。
$\therefore OB=6-2=4$，$OD=2$，$\therefore OD=\frac{1}{2}OB$，$\angle B=30^{\circ}$，$\angle DOB=60^{\circ}$。
$\therefore S_{\text{阴影}}=S_{\triangle ODB}-S_{\text{扇形}DOF}=\frac{1}{2}×2\sqrt{3}×2-\frac{60\pi×2^{2}}{360}=2\sqrt{3}-\frac{2\pi}{3}$。