21. (6分)如图,$\triangle ABC$的顶点都在方格纸的格点上,在方格纸内将$\triangle ABC$经过一次平移后得到$\triangle A'B'C'$,图中标出了点$B$的对应点$B'$.
(1)在给定方格纸中画出平移后的$\triangle A'B'C'$;
(2)画出$BC$边上的高$AD$;
(3)过点$C$画直线$l$,将$\triangle ABC$分成两个面积相等的三角形.

解:(1)如图,$\triangle A'B'C'$即为所求.
(2)如图,线段$AD$即为所求.
(3)如图,直线$l$即为所求.
(1)在给定方格纸中画出平移后的$\triangle A'B'C'$;
(2)画出$BC$边上的高$AD$;
(3)过点$C$画直线$l$,将$\triangle ABC$分成两个面积相等的三角形.

解:(1)如图,$\triangle A'B'C'$即为所求.
(2)如图,线段$AD$即为所求.
(3)如图,直线$l$即为所求.
答案:
21.
(1)如图,△A′B′C′即为所求.
(2)如图,线段AD即为所求.
(3)如图,直线l即为所求.

21.
(1)如图,△A′B′C′即为所求.
(2)如图,线段AD即为所求.
(3)如图,直线l即为所求.

22. (8分)先化简,再求值$(x - 2)^{2}+2(x + 2)(x - 4)-(x - 3)(x + 3)$,其中$x = -1$.
解:原式$=x^{2}-4x + 4+2x^{2}-4x - 16 - x^{2}+9=2x^{2}-8x - 3$,当$x = -1$时,原式$=2 + 8 - 3 = 7$.
解:原式$=x^{2}-4x + 4+2x^{2}-4x - 16 - x^{2}+9=2x^{2}-8x - 3$,当$x = -1$时,原式$=2 + 8 - 3 = 7$.
答案:
22.原式=x² - 4x + 4 + 2x² - 4x - 16 - x² + 9 = 2x² - 8x - 3,当x = -1时,原式=2 + 8 - 3 = 7.
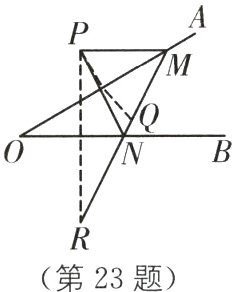
23. (10分)如图,点$P$是$\angle AOB$外的一点,点$M,N$分别是$\angle AOB$两边上的点,点$P$关于$OA$的对称点$Q$落在线段$M$上,点$P$关于$OB$的对称点$R$落在$MN$的延长线上,若$MN = a,QR = b$,其中$a\lt b$,试求$PN - PM$的值.(用$a$和$b$表示)
解:$\because$点$P$关于$OA$的对称点$Q$落在线段$MN$上,点$P$关于$OB$的对称点$R$落在$MN$上,$\therefore RN = PN,MQ = MP$,
$\therefore PN - PM = RN - MQ$,
$\therefore PN - PM=(RN + NQ)-(MQ + NQ)=QR - MN = b - a$.
解:$\because$点$P$关于$OA$的对称点$Q$落在线段$MN$上,点$P$关于$OB$的对称点$R$落在$MN$上,$\therefore RN = PN,MQ = MP$,
$\therefore PN - PM = RN - MQ$,
$\therefore PN - PM=(RN + NQ)-(MQ + NQ)=QR - MN = b - a$.

答案:
23.
∵点P关于OA的对称点Q落在线段MN上,点P关于OB的对称点R落在MN上,
∴RN = PN,MQ = MP,
∴PN - PM = RN - MQ,
∴PN - PM=(RN + NQ)-(MQ + NQ)=QR - MN = b - a.
∵点P关于OA的对称点Q落在线段MN上,点P关于OB的对称点R落在MN上,
∴RN = PN,MQ = MP,
∴PN - PM = RN - MQ,
∴PN - PM=(RN + NQ)-(MQ + NQ)=QR - MN = b - a.
24. (8分)将幂的运算逆向思维可以得到$a^{m + n}=a^{m}\cdot a^{n},a^{mn}=(a^{m})^{n},a^{n}b^{n}=(ab)^{n}$,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若$a^{m}=2,a^{n}=3$,求$a^{3m + 2n}$的值;
(2)若$2\times4^{x}\times8^{x}=2^{16}$,求$x$的值.
解:(1)根据题意可知,$a^{m}=2,a^{n}=3$,
$\therefore a^{3m + 2n}=a^{3m}\cdot a^{2n}=(a^{m})^{3}\cdot(a^{n})^{2}=2^{3}\times3^{2}=8\times9 = 72$.
(2)$\because 2\times4^{x}\times8^{x}=2\times(2^{2})^{x}\times(2^{3})^{x}=2^{1 + 2x + 3x}=2^{16}$,
$\therefore 1 + 2x + 3x = 16$,即$5x = 15$,解得$x = 3$.
(1)若$a^{m}=2,a^{n}=3$,求$a^{3m + 2n}$的值;
(2)若$2\times4^{x}\times8^{x}=2^{16}$,求$x$的值.
解:(1)根据题意可知,$a^{m}=2,a^{n}=3$,
$\therefore a^{3m + 2n}=a^{3m}\cdot a^{2n}=(a^{m})^{3}\cdot(a^{n})^{2}=2^{3}\times3^{2}=8\times9 = 72$.
(2)$\because 2\times4^{x}\times8^{x}=2\times(2^{2})^{x}\times(2^{3})^{x}=2^{1 + 2x + 3x}=2^{16}$,
$\therefore 1 + 2x + 3x = 16$,即$5x = 15$,解得$x = 3$.
答案:
24.
(1)根据题意可知,aᵐ = 2,aⁿ = 3,
∴a³ᵐ⁺²ⁿ=a³ᵐ·a²ⁿ=(aᵐ)³·(aⁿ)²=2³×3²=8×9 = 72;
(2)
∵2×4ˣ×8ˣ=2×(2²)ˣ×(2³)ˣ=2¹⁺²ˣ⁺³ˣ=2¹⁶,
∴1 + 2x + 3x = 16,即5x = 15,解得x = 3.
(1)根据题意可知,aᵐ = 2,aⁿ = 3,
∴a³ᵐ⁺²ⁿ=a³ᵐ·a²ⁿ=(aᵐ)³·(aⁿ)²=2³×3²=8×9 = 72;
(2)
∵2×4ˣ×8ˣ=2×(2²)ˣ×(2³)ˣ=2¹⁺²ˣ⁺³ˣ=2¹⁶,
∴1 + 2x + 3x = 16,即5x = 15,解得x = 3.
查看更多完整答案,请扫码查看


