6. 若$3^{x - 1}=27,2^{x}=4^{y - 1}$,则$x - y=( A )$.
A. 1
B. 0
C. 1.5
D. 2
A. 1
B. 0
C. 1.5
D. 2
答案:
6.A
7. $(-8)^{2024}+(-8)^{2023}$能被下列哪个数整除( C ).
A. 3
B. 5
C. 7
D. 9
A. 3
B. 5
C. 7
D. 9
答案:
7.C
8. (2024·宿迁泗洪期末)如图,分别将三角板$ABC$与$ADE$的一边$AB$与$AE$放置在直线$l$上,边$AC$与$AD$所在直线重合.现将三角板$ABC$绕点$A$逆时针旋转,三角板$ADE$绕点$A$顺时针旋转.当$AB$与$AE$第一次重合时,三角板停止运动.在旋转过程中,下列说法不正确的是( B ).
A. 当$AB$与$DE$垂直时,$\angle BAE = 150^{\circ}$
B. 当$BC$与$DE$平行时,$\angle BAE = 120^{\circ}$
C. 当$AC$与$DE$垂直时,$\angle BAE = 60^{\circ}$
D. 当$BC$与$AE$平行时,$\angle BAE = 45^{\circ}$
A. 当$AB$与$DE$垂直时,$\angle BAE = 150^{\circ}$
B. 当$BC$与$DE$平行时,$\angle BAE = 120^{\circ}$
C. 当$AC$与$DE$垂直时,$\angle BAE = 60^{\circ}$
D. 当$BC$与$AE$平行时,$\angle BAE = 45^{\circ}$
答案:
8.B [解析]当AB与DE垂直时,如图
(1),延长BA 交DE于点F,
由题意知∠AFE=90°,
∴∠EAF=180°−∠AFE−∠E=30°,
∴∠BAE=180°−∠EAF=150°,
∴A正确.

当BC与DE平行时,如图
(2),过点A作FQ//BC,则FQ//DE,
∴∠QAE=∠E=60°,∠BAQ=∠B=45°,
∴∠BAE=∠QAE+∠BAQ=105°,
∴B错误.
当AC与DE垂直时,如图
(3),延长CA交DE于点F,
∴AB//DE,
∴∠BAE=∠E=60°,
∴C正确.

当BC与AE平行时,如图
(4),
∴∠BAE=∠B=45°,
∴D正确.故选B.
8.B [解析]当AB与DE垂直时,如图
(1),延长BA 交DE于点F,
由题意知∠AFE=90°,
∴∠EAF=180°−∠AFE−∠E=30°,
∴∠BAE=180°−∠EAF=150°,
∴A正确.

当BC与DE平行时,如图
(2),过点A作FQ//BC,则FQ//DE,
∴∠QAE=∠E=60°,∠BAQ=∠B=45°,
∴∠BAE=∠QAE+∠BAQ=105°,
∴B错误.
当AC与DE垂直时,如图
(3),延长CA交DE于点F,
∴AB//DE,
∴∠BAE=∠E=60°,
∴C正确.

当BC与AE平行时,如图
(4),
∴∠BAE=∠B=45°,
∴D正确.故选B.
二、填空题(本题包括10小题,每小题3分,共30分)
答案:
9. PM2.5是指大气中直径小于或等于0.000 002 5 m的颗粒物,将0.000 002 5用科学记数法表示为 $2.5\times10^{-6}$.
答案:
9.2.5×10⁻⁶
10. 计算$(x + 3)(x + 4)-2(x + 6)$的结果为 $x^{2}+5x$.
答案:
10.x²+5x
11. 比较大小:$4^{30}\lt3^{40}$(填“$\gt$”“$\lt$”或“$=$”).
答案:
11.<
12. 若$a^{m}=4,a^{n}=2$,则$a^{2m - n}$的值为 8.
答案:
12.8
13. (2024·徐州沛县期中)在$(x - 2)(x^{2}-ax + 1)$计算结果中,不含$x^{2}$项,则$a$的值为 $-2$.
答案:
13.−2
14. 若$m + 2n - 3 = 0$,则$3^{m}\cdot9^{n}=27$.
答案:
14.27
15. (2024·泰州泰兴期末)小聪在学习完乘法公式后,发现完全平方公式经过适当的变形或数形结合,可以解决很多数学问题.如图摆放两个正方形卡片,$A,M,B$在同一直线上.若$AB = 5$,且两个正方形面积之和为13,则阴影部分的面积为 6.



答案:
15.6 [解析]如图,延长CD,EB交于点P,延长CA,EF交于点Q,易知四边形CPEQ为正方形,设正方形ACDM的边长为a,正方形BEFM的边长为b,

∵AB=5,两个正方形面积之和为13,
∴a + b = 5,a² + b² = 13,
S阴影部分=S正方形CPEQ - S△CFQ - S△CPB - S正方形BEFM
=(a + b)² - $\frac{1}{2}$a(a + b) - $\frac{1}{2}$a(a + b) - b²
=a² + 2ab + b² - a² - ab - b² = ab
=$\frac{(a + b)²-(a² + b²)}{2}$ = $\frac{25 - 13}{2}$ = 6.
15.6 [解析]如图,延长CD,EB交于点P,延长CA,EF交于点Q,易知四边形CPEQ为正方形,设正方形ACDM的边长为a,正方形BEFM的边长为b,

∵AB=5,两个正方形面积之和为13,
∴a + b = 5,a² + b² = 13,
S阴影部分=S正方形CPEQ - S△CFQ - S△CPB - S正方形BEFM
=(a + b)² - $\frac{1}{2}$a(a + b) - $\frac{1}{2}$a(a + b) - b²
=a² + 2ab + b² - a² - ab - b² = ab
=$\frac{(a + b)²-(a² + b²)}{2}$ = $\frac{25 - 13}{2}$ = 6.
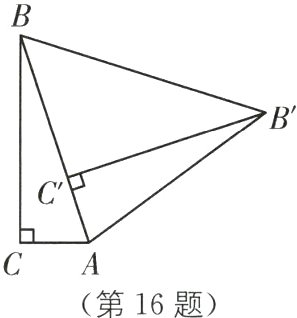
16. (2024·苏州期末)如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,将$Rt\triangle ABC$绕顶点$A$顺时针旋转一定角度得到$Rt\triangle AB'C'$,此时点$C$的对应点$C'$恰好落在$AB$边上,连接$BB'$,若$\angle BB'C' = 35^{\circ}$,则$\angle BAC = 70^{\circ}$.
答案:
16.70 [解析]
∵将Rt△ABC绕顶点A顺时针旋转一定角度得到Rt△AB'C',此时点C的对应点C'恰好落在AB边上,
∴AB = AB',∠BC'B' = 90°,∠B'AC' = ∠BAC,
∴∠ABB' = ∠AB'B.
又∠BB'C' = 35°,
∴∠ABB' = 90° - 35° = 55°,
∴∠BAC = ∠B'AC' = 180° - 55°×2 = 70°.
∵将Rt△ABC绕顶点A顺时针旋转一定角度得到Rt△AB'C',此时点C的对应点C'恰好落在AB边上,
∴AB = AB',∠BC'B' = 90°,∠B'AC' = ∠BAC,
∴∠ABB' = ∠AB'B.
又∠BB'C' = 35°,
∴∠ABB' = 90° - 35° = 55°,
∴∠BAC = ∠B'AC' = 180° - 55°×2 = 70°.
查看更多完整答案,请扫码查看


